Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

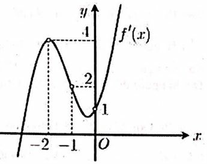
Xét hàm số có
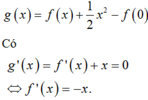
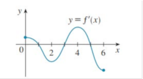
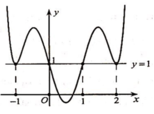
Vẽ đồ thị hàm số y = f ' x và đường thẳng y = - x trên cùng mặt phẳng tọa độ ta có:
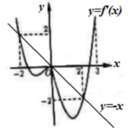
Khi đó ta có
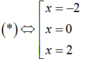
Phương trình g ' x = 0 có 1 nghiệm đơn x = 2 ∈ - 2 ; 3 ⇒ Hàm số y = g x có 1 cực trị thuộc - 2 ; 3
Xét
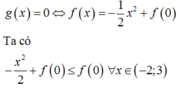
BBT hàm số y = f x
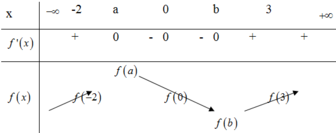
Ta so sánh f(0) và f(3)
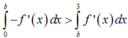
![]()
![]()
So sánh f(0) và f(-2). Ta có:
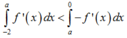
![]()
![]()
Phương trình f x = - x 2 2 + f 0 có tối đa nghiệm thuộc - 2 ; 3
Phương trình g x = 0 có tối đa 2 nghiệm ⇒ Hàm số y = g x có tối đa 1 + 2 = 3 cực trị
Chọn D.

Đáp án B.
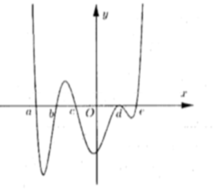
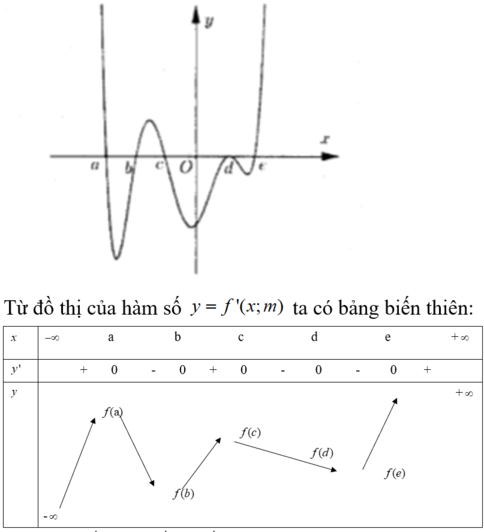
Từ đồ thị hàm số y = f ' ( x ) ta có bảng biến thiên:

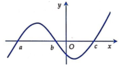
Từ bảng biến thiên ta có f ( b ) > f ( a ) > 0
Quan sát đồ thị y = f ' ( x ) , dùng phương pháp tích phân để tính diện tích.
Ta có ∫ a b f ' ( x ) d x < ∫ a c 0 - f ' ( x ) d x ⇒ f ( c ) < f a
Nếu f c < 0 thì đồ thị hàm số y = f ( x ) cắt trục hoành tại 2 điểm phân biệt.
Nếu f c = 0 thì đồ thị hàm số y = f ( x ) tiếp xúc với trục hoành tại 1 điểm.
Nếu f c > 0 thì đồ thị hàm số y = f ( x ) không cắt trục hoành.
Vậy đồ thị hàm số y = f ( x ) cắt trục hoành tại nhiều nhất 2 điểm.

Đáp án A
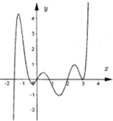
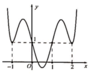
Phương trình f ' (x) = 0 có 3nghiệm,trong đó có 2 nghiệm kép do tiếp xúc. Dạng phương trình f ' ( x ) = x - x 1 2 x - x 2 . Do đó hàm số y = f(x) có duy nhất một điểm cực trị.
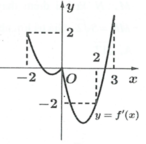









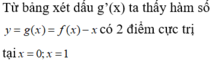
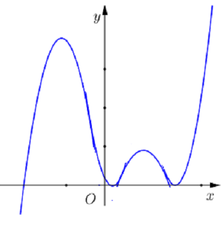
Chọn D
Suy ra hàm số g(x) có một điểm cực trị thuộc khoảng (-2;3)
● n là số nghiệm đơn hoặc bội lẻ của phương trình g(x) = 0 trên (-2;3)
Lại có g’(x) = 0 có một điểm cực trị => g(x) = 0 có nhiều nhất 2 nghiệm
Vậy hàm số đã cho có nhiều nhất 3 điểm cực trị.