

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Chọn D
* Tập xác định ![]()
* Ta có 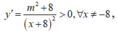
suy ra hàm số đã cho đồng biến trên đoạn [0;3].
Do đó 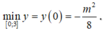
* Theo yêu cầu bài toán ta có: 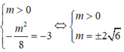
![]()

a) y = f(x) = x3 – 3mx2 + 3(2m-1)x + 1
Tập xác định: D = R
y’= 3x2 -6mx + 3(2m-1) = 3(x2 – 2mx + 2m – 1)
Hàm số đồng biến trên D = R ⇔ y’ ≥ 0, ∀x ∈ R
⇔ x2 – 2mx + 2m - 1≥0, ∀x ∈ R
⇔ Δ’ = m2 – 2m + 1 = (m-1)2 ≤ 0 ⇔ m =1
b) Hàm số có một cực đại và một cực tiểu
⇔ phương trình y’= 0 có hai nghiệm phân biệt
⇔ (m-1)2 > 0 ⇔ m≠1
c) f’’(x) = 6x – 6m > 6x
⇔ -6m > 0 ⇔ m < 0

\(f'\left(x\right)=m^2x^4-mx^2+20x-\left(m^2-m-20\right)\)
Để hàm số đồng biến trên \(ℝ\)thì \(f'\left(x\right)\ge0,\)với mọi \(x\inℝ\).
Mà ta thấy \(f'\left(-1\right)=m^2-m-20-\left(m^2-m-20\right)=0\)
do đó \(x=-1\)là một điểm cực trị của hàm số \(f'\left(x\right)\).
Ta có: \(f''\left(x\right)=4m^2x^3-2mx+20\)
\(f''\left(-1\right)=0\Leftrightarrow-4m^2+2m+20=0\Leftrightarrow\orbr{\begin{cases}m=\frac{5}{2}\\m=-2\end{cases}}\).
Thử lại.
Với \(m=\frac{5}{2}\): \(f''\left(x\right)=25x^3-5x+20\)
\(f''\left(x\right)=0\Leftrightarrow x=-1\)
\(f'\left(-1\right)=0\)
do đó \(f'\left(x\right)\ge0\)thỏa mãn.
Với \(m=-2\): \(f''\left(x\right)=16x^3+4x+20\)
\(f''\left(x\right)=0\Leftrightarrow x=-1\).
\(f'\left(-1\right)=0\)
do đó \(f'\left(x\right)\ge0\)thỏa mãn.
Vậy tổng các giá trị của \(m\)là: \(\frac{5}{2}+\left(-2\right)=\frac{1}{2}\).
Chọn D.

Đạo hàm f'(x) = m 2 - m + 1 ( x + 1 ) 2 > 0, ∀ x ∈ [ 0 ; 1 ]
Suy ra hàm số f(x) đồng biến trên [0; 1] nên min f(x) = f(0) = -m2+m
Theo bài ta có:
-m2+ m= -2 nên m= -1 hoặc m= 2.
Chọn D.

Ta có \(y'=3\left(x^2-m\right)\Rightarrow y'=0\Leftrightarrow x^2=m\)
Hàm số có 2 cực trị khi và chỉ khi \(m>0\). Khi đó tọa độ 2 điểm A, B là :
\(A\left(\sqrt{m}'-2m\sqrt{m}\right);B\left(-\sqrt{m};2m\sqrt{m}+2\right)\)
Suy ra \(\overrightarrow{AB}=\left(-2\sqrt{m};4m\sqrt{m}\right)\Rightarrow\overrightarrow{n}\left(2m;1\right)\) là vecto pháp tuyến của AB
Phương trình AB : 2mx + y -2 = 0
Suy ra \(d\left(I,AB\right)=\frac{\left|2m-1\right|}{\sqrt{1-4m^2}},AB=2\sqrt{m}.\sqrt{1+4m^2}\)
Do đó \(S_{\Delta IAB}=\frac{1}{2}.AB.d\left(I,AB\right)=\sqrt{m}\left|2m-1\right|\)
Mà \(S_{\Delta IAB}=\sqrt{18}\Rightarrow\sqrt{m}\left|2m-1\right|=\sqrt{18}\Rightarrow4m^3-4m^2+m-18=0\Leftrightarrow m=2\)
Vậy m = 2 là giá trị cần tìm

f'(x)>0 với mọi x khác -8, suy ra hàm số đã cho đồng biến trên [0;3].
Giá trị nhỏ nhất của f(x) trên [0;3] là (-m^2)/8. Ta có: (-m^2)/8=2.
Suy ra, không có giá trị nào của số thực m thỏa yêu cầu đề bài.