Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

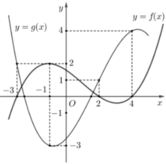
Đặt t =f(x) ta có f[f(x)]=1→f(t)=1
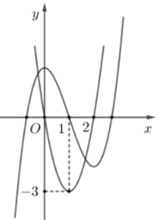
Dựa vào sự tương giao của đồ thị hàm số y=f(x) và đường thẳng y=1 ta thấy phương trình f(t)=1 có 3 nghiệm t =a ϵ (0 ;2),t =c ϵ(2 ;+∞) Dựa vào đồ thị ta lại có:
Phương trình t =a→f(x) =a và phương trình t =f(x) =b có 3 nghiệm phâ biệt.
Phương trình f =f(x) =c có một nghiệm duy nhất.
Vậy phương trình đã cho có 7 nghiệm .
Chọn đáp án B.

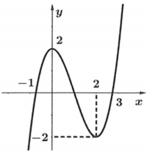
Đồ thị hàm số |f(x)| được suy ra từ đồ thị hàm số f(x) bằng cách:
Giữ nguyên phần đồ thị hàm số f(x) phía trên trục hoành;
Lấy đối xứng qua trục hoành phần đồ thị phía dưới trục hoành của hàm số f(x)
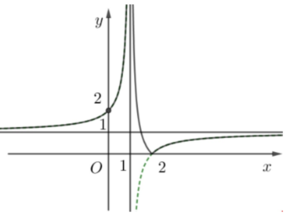
Quan sát đồ thị suy ra phương trình |f(x)=m có hai nghiệm thực phân biệt
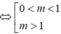
Chọn đáp án D.

Đáp án B
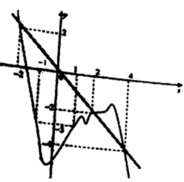
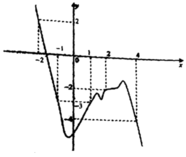
Phương pháp: Lập bảng biến thiên của g(x) và đánh giá số giao điểm của đồ thị hàm số y = g(x) và trục hoành.
Cách giải: 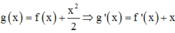
![]()
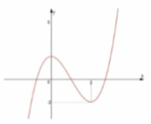
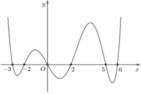
Xét giao điểm của đồ thị hàm sốy = f’(x) và đường thẳng y = -x ta thấy, hai đồ thị cắt nhau tại ba điểm có hoành độ là: -2;2;4 tương ứng với 3 điểm cực trị của y = g(x).
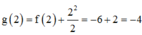
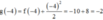
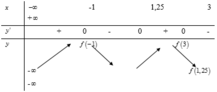
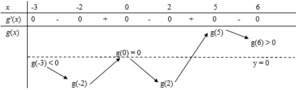
Bảng biến thiên:
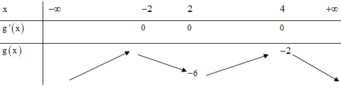
Dựa vào bảng biến thiên ta thấy ![]() => phương trình g(x) = 0 không có nghiệm
=> phương trình g(x) = 0 không có nghiệm ![]()

Ta có ![]()
![]()
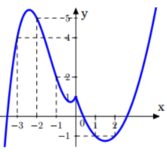
Quan sát đồ thị có 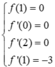
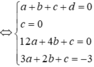

![]()
Đặt ![]() phương trình trở thành:
phương trình trở thành:
![]()
![]()
![]()
Khi đó ![]()
Phương trình này có 3 nghiệm phân biệt
![]()
Tổng các phần tử củaS bằng 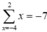
Chọn đáp án C.
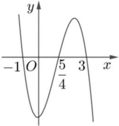
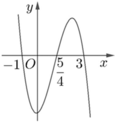
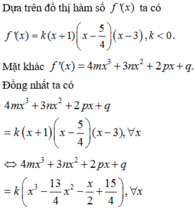
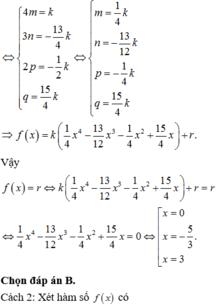
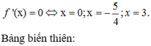


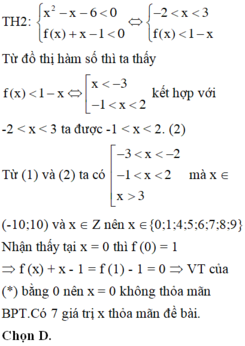


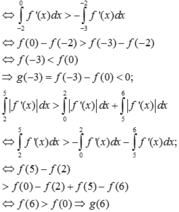
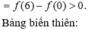


Đáp án là B