Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có: \(\overrightarrow a .\overrightarrow b = \left| {\overrightarrow a } \right|.\left| {\overrightarrow b } \right|.\cos \left( {\overrightarrow a ,\overrightarrow b } \right)\)
\( \Leftrightarrow 12\sqrt 2 = 3.8.\cos \left( {\overrightarrow a ,\overrightarrow b } \right) \Leftrightarrow \cos \left( {\overrightarrow a ,\overrightarrow b } \right) = \frac{{\sqrt 2 }}{2}\)
\( \Rightarrow \left( {\overrightarrow a ,\overrightarrow b } \right) = 45^\circ \)
Vậy góc giữa hai vectơ \(\overrightarrow a \) và \(\overrightarrow b \) là \(45^\circ \)

Ta có: \(\overrightarrow u = \left( {0; - 5} \right),\;\overrightarrow v = \left( {\sqrt 3 ;1} \right)\)
\( \Rightarrow \overrightarrow u .\;\,\overrightarrow v = 0.\sqrt 3 + \left( { - 5} \right).1 = - 5.\)

a) I là tâm của ABCD, suy ra \(\widehat {IDC} = 45^\circ \)
b) Vectơ có điểm đầu là D và điểm cuối là I là \(\overrightarrow {DI} \)
Vectơ có điểm đầu là D và điểm cuối là C là \(\overrightarrow {DC} \)
c) Vectơ có điểm đầu là D và bằng vectơ \(\overrightarrow {IB} \) là \(\overrightarrow {DI} \)
Vectơ có điểm đầu là D và bằng vectơ \(\overrightarrow {AB} \) là \(\overrightarrow {DC} \)

Gọi vectơ chỉ vận tốc của máy bay là vectơ \(\overrightarrow {AB} \) và vectơ chỉ vận tốc của gió là vectơ \(\overrightarrow {BC} \).
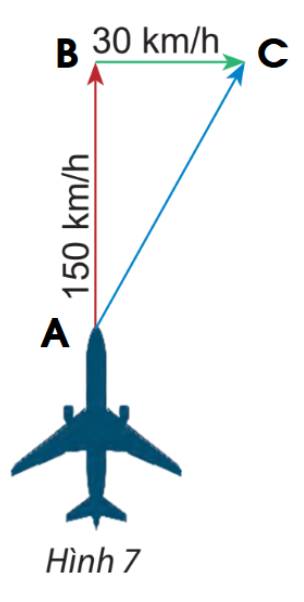
Ta có: \(\overrightarrow {AB} + \overrightarrow {BC} = \overrightarrow {AC} \)
Áp dụng định lý Pitago ta có:
\(AC = \sqrt {A{B^2} + B{C^2}} = \sqrt {{{150}^2} + {{30}^2}} = 30\sqrt {26} \)
Vậy độ dài vectơ tổng của hai vectơ nói trên là \(30\sqrt {26} \) km/h


Áp dụng quy tắc hình bình hành ta có: \(\overrightarrow F = \overrightarrow {{F_1}} + \overrightarrow {{F_2}} = \overrightarrow {OA} + \overrightarrow {OB} = \overrightarrow {OC} \);
\(AC = OB = 600\); \(\widehat {AOB} = 60^\circ \Rightarrow \widehat {OAC} = 120^\circ \) (hai góc bù nhau trong hình bình hành).
Áp dụng định lý cos ta có:
\(OC = \sqrt {O{A^2} + A{C^2} - 2OA.AC.\cos (120^\circ )} \)
\( = \sqrt {{{400}^2} + {{600}^2} - 2.400.600.\cos (120^\circ )} \simeq 871,78\)N
Vậy độ lớn của vectơ hợp lực \(\overrightarrow F \) gần bằng 871,78 N.

Chọn C.
Áp dụng hệ quả của định lí cosin ta có
![]()
Do đó; góc giữa 2 vecto đã cho là 450.
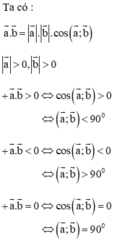


Ta cho: \(\left| {\overrightarrow a } \right| = 3;\left| {\overrightarrow b } \right| = 4\) và \(\overrightarrow a .\overrightarrow b = - 6\)
Ta có công thức:
\(\overrightarrow a .\overrightarrow b = \left| {\overrightarrow a } \right|.\left| {\overrightarrow b } \right|.\cos \left( {\overrightarrow a ,\overrightarrow b } \right) = 3.4.\cos \left( {\overrightarrow a ,\overrightarrow b } \right)\)
\(\overrightarrow a .\overrightarrow b = - 6 \Rightarrow 3.4.\cos \left( {\overrightarrow a ,\overrightarrow b } \right) = - 6 \Rightarrow \cos \left( {\overrightarrow a ,\overrightarrow b } \right) = - \frac{1}{2}\)
\( \Rightarrow \left( {\overrightarrow a ,\overrightarrow b } \right) = 120^\circ \)