Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Tứ giác \(AEHF\)có: \(\widehat{HEA}=\widehat{EAF}=\widehat{AFH\:}=90^0\)
\(\Rightarrow\)\(AEHF\) là hình chữ nhật
b) Xét \(\Delta BEH\)và \(\Delta AHC\)ta có:
\(\widehat{BEH}=\widehat{AHC}=90^0\)
\(\widehat{EBH}=\widehat{HAC}\) (cùng phụ với góc HAB)
suy ra: \(\Delta BEH~\Delta AHC\)
\(\Rightarrow\)\(\frac{BE}{AH}=\frac{EH}{HC}\)
\(\Rightarrow\)\(BE.HC=AH.EH\) (đpcm)

a: Xét ΔAHC vuông tại H có HK là đường cao ứng với cạnh huyền AB
nên \(AK\cdot AC=AH^2\left(1\right)\)
Xét ΔACB vuông tại A có AH là đường cao ứng với cạnh huyền AC
nên \(HB\cdot HC=AH^2\left(2\right)\)
Từ (1) và (2) suy ra \(AK\cdot AC=HB\cdot HC\)

Qua H kẻ đường thẳng song song với EC cắt AB tại F. Sử dụng định lý đường trung bình của tam giác chứng minh được F là trung điểm của BE và

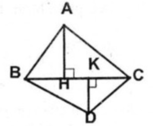


Hai △ ABC và △ DBC có chung canh đáy BC nên ta có:
S A B C = 1/2 AH. BC = S
S D B C = 1/2 DK. BC = S'