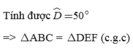
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
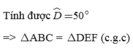
\(\widehat{D}=180^0-\widehat{E}-\widehat{F}=50^0=\widehat{A}\\ \left\{{}\begin{matrix}AB=DE\\\widehat{A}=\widehat{D}\\AC=DE\end{matrix}\right.\Rightarrow\Delta ABC=\Delta DEF\left(c.g.c\right)\)
Xét t/giác DEF có \(\widehat{D}+\widehat{E}+\widehat{F}=180^0\) (tổng 3 góc của 1 t/giác)
=> \(\widehat{D}=180^0-\widehat{E}-\widehat{F}=180^0-70^0-60^0=50^0\)
Xét t/giác ABC và t/giác DEF
có: AB = DE (gt)
AC = DF (gt)
\(\widehat{A}=\widehat{D}=50^0\)
=> t/giác ABC = t/giác DEF (c.g.c)
Xét \(\Delta DEF\) có:
\(\widehat{D}+\widehat{E}+\widehat{F}=180^0\) (định lí tổng 3 góc trong một tam giác).
=> \(\widehat{D}+70^0+60^0=180^0\)
=> \(\widehat{D}+130^0=180^0\)
=> \(\widehat{D}=180^0-130^0\)
=> \(\widehat{D}=50^0.\)
Mà \(\widehat{A}=50^0\left(gt\right)\)
=> \(\widehat{D}=\widehat{A}=50^0.\)
Xét 2 \(\Delta\) \(ABC\) và \(DEF\) có:
\(AB=DE\left(gt\right)\)
\(\widehat{A}=\widehat{D}\left(cmt\right)\)
\(AC=DF\left(gt\right)\)
=> \(\Delta ABC=\Delta DEF\left(c-g-c\right)\left(đpcm\right).\)
Chúc bạn học tốt!
Khẳng định sai là :
C.nếu AB=DE và B=E thì hai tam giác trên bằng nhau
# học tốt #
a: Xét ΔADB và ΔADC có
AB=AC
góc BAD=góc CAD
AD chung
=>ΔADB=ΔADC
b: Xét ΔAED vuông tại E và ΔAFD vuông tại F có
AD chung
góc EAD=góc FAD
=>ΔAED=ΔAFD
=>AE=AF và DE=DF
c: Xét ΔABC có AE/AB=AF/AC
nên EF//BC
