Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Năm số hạng đầu của dãy số là 3, √10, √11, √12, √13.
b) Ta có: u1 = 3 = √9 = √(1 + 8)
u2 = √10 = √(2 + 8)
u3 = √11 = √(3 + 8)
u4 = √12 = √(4 + 8)
...........
Từ trên ta dự đoán un = √(n + 8), với n ε N* (1)
Chứng minh công thức (1) bằng phương pháp quy nạp:
- Với n = 1, rõ ràng công thức (1) là đúng.
- Giả sử (1) đúng với n = k ≥ 1, tức là có uk = √(k + 8) với k ≥ 1.
Theo công thức dãy số, ta có:
uk+1 = .
Như vậy công thức (1) đúng với n = k + 1.

a) Năm số hạng đầu của dãy số là 3, √10, √11, √12, √13.
b) Ta có: u1 = 3 = √9 = √(1 + 8)
u2 = √10 = √(2 + 8)
u3 = √11 = √(3 + 8)
u4 = √12 = √(4 + 8)
...........
Từ trên ta dự đoán un = √(n + 8), với n ε N* (1)
Chứng minh công thức (1) bằng phương pháp quy nạp:
- Với n = 1, rõ ràng công thức (1) là đúng.
- Giả sử (1) đúng với n = k ≥ 1, tức là có uk = √(k + 8) với k ≥ 1.
Theo công thức dãy số, ta có:
uk+1 = .
Như vậy công thức (1) đúng với n = k + 1.

a) Ta có:
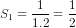
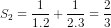
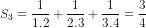
b) Từ câu a) ta dự đoán 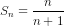 (1), với mọi n ε N* .
(1), với mọi n ε N* .
Ta sẽ chứng minh đẳng thức (1) bằng phương pháp quy nạp
Khi n = 1, vế trái là 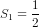 , vế phải bằng
, vế phải bằng 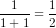 . Vậy đẳng thức (1) đúng.
. Vậy đẳng thức (1) đúng.
Giả sử đẳng thức (1) đúng với n = ≥ 1, tức là
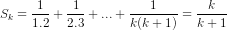
Ta phải chứng minh nó cũng đúng khi n = k + 1, nh=ghĩa là phải chứng minh
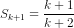
Ta có 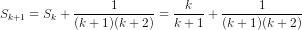
= 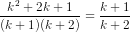
tức là đẳng thức (1) cũng đúng với n = k + 1.
Vậy điều cần chứng minh đúng với mọi n.

a. Năm số hạng đầu của dãy số
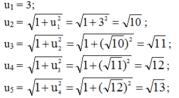
b. Dự đoán công thức số hạng tổng quát của dãy số:
un =√(n+8) (1)
Rõ ràng (1) đúng với n = 1
Giả sử (1) đúng với n = k, nghĩa là uk = √(k+8)
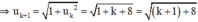
⇒ (1) đúng với n = k + 1
⇒ (1) đúng với mọi n ∈ N*.

a)
Với \(n=1\).
\(n^5-n=1^5-1=0\).
Do 0 chia hết cho 5 nên điều cần chứng minh đúng với n = 1.
Giả sử điều cần chứng minh đúng với \(n=k\).
Nghĩa là: \(k^5-k⋮5\).
Ta cần chứng minh nó đúng với \(n=k+1\).
Nghĩa là: \(\left(k+1\right)^5-\left(k+1\right)⋮5\).
Thật vậy:
\(\left(k+1\right)^5-\left(k+1\right)=C^0_5k^0+C^1_5k+...+C^5_5k^5-k-1\)
\(=1+C^1_5k+...+k^5-k-1\)
\(=C^1_5k+...+C^4_5k^4+k^5-k\)
Do mỗi \(C_5^1;C^2_5;C^3_5;C^4_5\) đều chia hết cho 5 và do gải thiết quy nạp \(k^5-k⋮5\) nên \(C^1_5k+...+C^4_5k^4+k^5-k\) chia hết cho 5.
Vì vậy: \(\left(k+1\right)^5-\left(k+1\right)⋮5\).
Vậy điều phải chứng minh đúng với mọi n.
b)
Tổng bình phương 3 số tự nhiên liên tiếp là: \(n^3+\left(n+1\right)^3+\left(n+2\right)^3\).
Ta cần chứng minh \(n^3+\left(n+1\right)^3+\left(n+2\right)^3⋮9,\forall n\in N^{\circledast}\).
Với n = 1.
\(n^3+\left(n+1\right)^3+\left(n+2\right)^3=1^3+2^3+3^3=36\).
Vậy điều cần chứng minh đúng với \(n=1\).
Giả sử điều cần chứng minh đúng với n = k.
Nghĩa là: \(k^3+\left(k+1\right)^3+\left(k+2\right)^3⋮9\).
Ta cần chứng minh nó đúng với \(n=k+1\).
Nghĩa là: \(\left(k+1\right)^3+\left(k+2\right)^3+\left(k+3\right)^3⋮9\)
Thật vậy:
\(\left(k+1\right)^3+\left(k+2\right)^3+\left(k+3\right)^3\)\(=\left(k+1\right)^3+\left(k+2\right)^3+k^3+3.3k^2+3.k.3^2+3^3\)
\(=\left(k+1\right)^3+\left(k+2\right)^3+k^3+9k^2+27k+81\)
Theo giả thiết quy nạp \(k^3+\left(k+1\right)^3+\left(k+2\right)^3⋮9\) và \(9k^2+27k+81=9\left(k^2+3k+9\right)⋮9\).
Nên \(\left(k+1\right)^3+\left(k+2\right)^3+k^3+9k^2+27k+81⋮9\).
Vậy điều phải chứng minh đúng với mọi n.

a)
Với \(n=4\).
\(3^{n-1}=3^{4-1}=3^3=27\); \(n\left(n+2\right)=4.\left(4+2\right)=24\).
Suy ra: \(3^{n-1}>n\left(n+2\right)\) với n = 4.
Giả sử điều phải chứng minh đúng với \(n=k\).
Nghĩa là: \(3^{k-1}>k\left(k+2\right)\).
Ta sẽ chứng minh nó đúng với \(n=k+1\).
Nghĩa là:
\(3^{k+1-1}>\left(k+1\right)\left(k+1+2\right)\)\(\Leftrightarrow3^k>\left(k+1\right)\left(k+3\right)\).
Thật vậy từ giả thiết quy nạp ta có:
\(3^k=3.3^{k-1}>3k\left(k+2\right)=3k^2+6k\)\(=k^2+4k+3+2k^2+2k-3\)\(=\left(k+1\right)\left(k+3\right)+2k^2+2k-3\).
Với \(k\in N^{\circledast}\) thì \(2k^2+2k-3>0\) nên \(3^k>\left(k+1\right)\left(k+3\right)\).
Vậy điều cần chứng minh đúng với mọi \(n\ge4\).
b)
Với \(n=8\)
\(2^{n-3}=2^{8-3}=2^5=32\); \(3n-1=3.8-1=23\).
Vậy điều cần chứng minh đúng với \(n=8\).
Giả sử điều cần chứng minh đúng với \(n=k\left(k\ge8\right)\).
Nghĩa là: \(2^{k-3}>3k-1\).
Ta sẽ chứng minh nó cũng đúng với \(n=k+1\).
Nghĩa là: \(2^{k+1-3}>3\left(k+1\right)-1\)\(\Leftrightarrow2^{k-2}>3k+2\).
Thật vậy \(2^{k-2}=2.2^{k-3}>2\left(3k-1\right)=6k-2\)\(=3k+2+3k-4\).
Do \(k\ge8\) nên \(k-4>0\) vì vậy \(2^{k-2}>3k+2\).
Vậy điều cần chứng minh đúng với mọi \(n\ge8\).

Đề bài không rõ ràng. n ở đây là tự nhiên, nguyên hay là chơi luôn cả R
a)n = 1 ⇒ 31 = 3 < 8 = 8.1
n = 2 ⇒ 32 = 9 < 16 = 8.2
n = 3 ⇒ 33 = 27 > 24 = 8.3
n = 4 ⇒ 34 = 81 > 32 = 8.4
n = 5 ⇒ 35 = 243 > 40 = 8.5
b) Dự đoán kết quả tổng quát: 3n > 8n với mọi n ≥ 3
- n = 3, bất đẳng thức đúng
- Giả sử bất đẳng thức đúng với n = k ≥ 3, nghĩa là:
3k > 8k
Ta phải chứng minh rằng bất đẳng thức cũng đúng với n = k + 1, tức là:
3(k + 1) > 8(k + 1)
Thật vậy, từ giả thiết quy nạp ta có:
3(k + 1) = 3k.3 > 8k.3 = 24k = 8k + 16k
k ≥ 3 ⇒ 16k ≥ 16.3 = 48 > 8
Suy ra: 3(k + 1) > 8k + 8 = 8(k + 1)
Vậy bất đẳng thức đúng với mọi n ≥ 3