Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

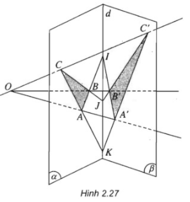
a) I, A’, B’ là ba điểm chung của hai mặt phẳng (OAB) và (β) nên chúng thẳng hàng.
b) I, J, K là ba điểm chung của hai mặt phẳng (ABC) và (A’B’C’) nên chúng thẳng hàng.

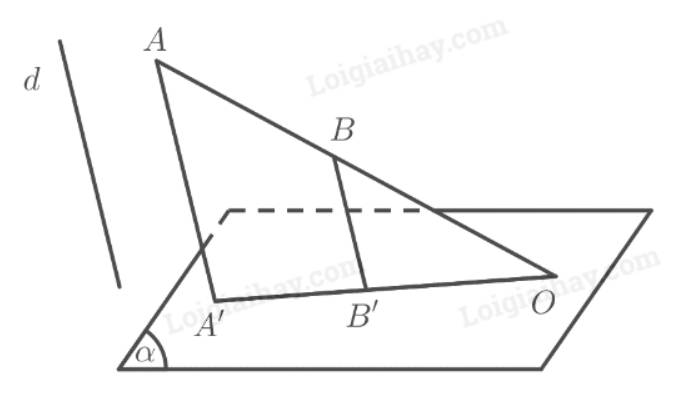
Vì \(O \in \left( \alpha \right)\) nên \(O\) là hình chiếu của chính nó lên mặt phẳng \(\left( \alpha \right)\) theo phương \(d\).
Vì ba điểm \(O,A,B\) thẳng hàng nên ba điểm \(O,A',B'\) thẳng hàng.
\(AA'\parallel BB' \Rightarrow \frac{{AB}}{{OA}} = \frac{{A'B'}}{{OA'}} \Leftrightarrow \frac{{A'B'}}{{AB}} = \frac{{OA'}}{{OA}}\)
a) Để \(A'B' = AB\) thì \(OA' = OA\).
Vậy đường thẳng \(d\) song song với \(AA'\) và \(OA' = OA\).
b) Để \(A'B' = 2AB\) thì \(OA' = 2OA\).
Vậy đường thẳng \(d\) song song với \(AA'\) và \(OA' = 2OA\).

a) S, I, J, G là điểm chunng của (SAE) và (SBD)
b) S, K, L là điểm chung của (SAB) và (SDE)

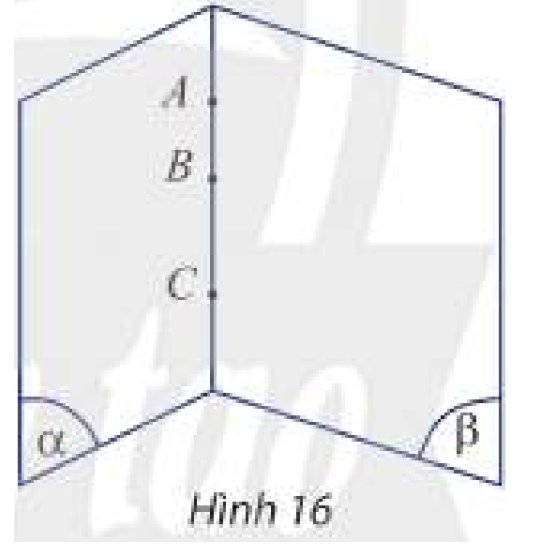
Ta có: \(A,B,C\) là ba điểm chung của hai mặt phẳng phân biệt \(\left( \alpha \right)\) và \(\left( \beta \right)\) nên \(A,B,C\) cùng nằm trên giao tuyến của hai mặt phẳng \(\left( \alpha \right)\) và \(\left( \beta \right)\) (theo tính chất 5).
Vậy \(A,B,C\) thẳng hàng.

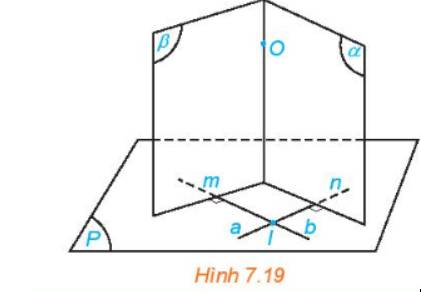
a) Vì \(\left( \alpha \right),\left( \beta \right)\) là các mặt phẳng qua O và giao 2 mặt phẳng là 1 đường thẳng nên hai mặt phẳng \(\left( \alpha \right),\left( \beta \right)\) cắt nhau theo một đường thẳng đi qua O.
b) Gọi \(\Delta \) là giao tuyến của 2 \(\left( \alpha \right),\left( \beta \right)\)
\(\left. \begin{array}{l}a \bot \left( \alpha \right)\\\Delta \subset \left( \alpha \right)\end{array} \right\} \Rightarrow a \bot \Delta \)
\(\left. \begin{array}{l}b \bot \left( \beta \right)\\\Delta \subset \left( \beta \right)\end{array} \right\} \Rightarrow b \bot \Delta \)
Mà \(a \cap b = \left\{ I \right\} \Rightarrow \Delta \bot \left( P \right)\)