Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

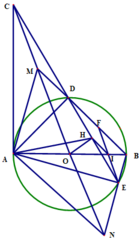
a) Ta có
C A B ⏜ = 90 0 O H C ⏜ = 90 0 ⇒ C A B ⏜ + O H C ⏜ = 180 0
Vậy tứ giác AOHC nội tiếp.
b) Ta có C A D ⏜ = A E C ⏜ , A C E ⏜ chung suy ra Δ A C D ~ Δ E C A (g.g)
⇒ C A C E = A D A E ⇒ A C . A E = A D . C E
c) Từ E vẽ đường thẳng song song với MN cắt cạnh AB tại I và cắt cạnh BD tại F ⇒ H E I ⏜ = H C O ⏜ .
Vì tứ giác AOHC nội tiếp ⇒ H A O ⏜ = H C O ⏜ = H E I ⏜ .
Suy ra tứ giác AHIE nội tiếp ⇒ I H E ⏜ = I A E ⏜ = B D E ⏜ ⇒ H I / / B D .
Mà H là trung điểm của DE=> I là trung điểm của EF. Có EF//MN và IE= IF
=> O là trung điểm của đoạn thẳng MN.
Suy ra tứ giác AMBN là hình bình hành => AM//BN.

Xét ΔMC'A và ΔMBD' có
góc MC'A=góc MBD'
góc M chung
=>ΔMC'A đồng dạng với ΔMBD'
=>MC'/MB=MA/MD'
=>MC'*MD'=MA*MB
Xét ΔMAC và ΔMDB có
góc MAC=góc MDB
góc M chung
=>ΔMAC đồng dạng với ΔMDB
=>MA/MD=MC/MB
=>MA*MB=MD*MC
=>MD*MC=MC'*MD'
=>MD/MC'=MD'/MC
=>ΔMDD' đồng dạng với ΔMC'C
=>góc MDD'=góc MC'C
=>góc D'C'C+góc D'DC=180 độ
=>CDC'D' nội tiếp

A B O M I C D E F
MO là trung trực của AI => MO vuông góc AI, có BI vuông góc AI => MO || BI
Ta thấy MA.MI là hai tiếp tuyến kẻ từ M đến (O), MCD là cát tuyến của (O), do đó \(\left(ICAD\right)=-1\)
Vì B nằm trên (O) nên \(B\left(ICAD\right)=-1\), mà MO || BI, MO cắt BC,BA,BD tại E,O,F nên O là trung điểm EF.


Xét tứ giác ACDB có A,C,D,B cùng nằm trên (O)
nên ACDB là tứ giác nội tiếp
=>\(\widehat{CAB}+\widehat{CDB}=180^0\)
mà \(\widehat{CAB}+\widehat{MAC}=180^0\)(hai góc kề bù)
nên \(\widehat{MAC}=\widehat{CDB}=\widehat{MDB}\)
Xét tứ giác AEFB có A,E,F,B cùng nằm trên (O')
nên AEFB là tứ giác nội tiếp
=>\(\widehat{BAE}+\widehat{BFE}=180^0\)
mà \(\widehat{BAE}+\widehat{MAE}=180^0\)(hai góc kề bù)
nên \(\widehat{MAE}=\widehat{MFB}\)
Xét ΔMCA và ΔMBD có
\(\widehat{MAC}=\widehat{MDB}\)
\(\widehat{M}\) chung
Do đó: ΔMCA đồng dạng với ΔMBD
=>\(\dfrac{MC}{MB}=\dfrac{MA}{MD}\)
=>\(MC\cdot MD=MA\cdot MB\)(1)
Xét ΔMAE và ΔMFB có
\(\widehat{MAE}=\widehat{MFB}\)
\(\widehat{M}\) chung
Do đó: ΔMAE đồng dạng với ΔMFB
=>\(\dfrac{MA}{MF}=\dfrac{ME}{MB}\)
=>\(MA\cdot MB=MF\cdot ME\left(2\right)\)
Từ (1) và (2) suy ra \(MC\cdot MD=ME\cdot MF\)
=>\(\dfrac{MC}{MF}=\dfrac{ME}{MD}\)
Xét ΔMCE và ΔMFD có
\(\dfrac{MC}{MF}=\dfrac{ME}{MD}\)
\(\widehat{CME}\) chung
Do đó: ΔMCE đồng dạng với ΔMFD
=>\(\widehat{MCE}=\widehat{MFD}\)
mà \(\widehat{MCE}+\widehat{DCE}=180^0\)(hai góc kề bù)
nên \(\widehat{MFD}+\widehat{DCE}=180^0\)
=>CDFE là tứ giác nội tiếp