Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bạn tự vẽ hình nha
a, vì NM=NE nên góc NEM=NME 1 mà xx' song song với yy' nên xME = MEN 2
Từ 1,2 xME=EMN. Tương tự NEF = xMF
b, theo câu a ME MF là tia p/g nên xMN+ NMx = 180 độ nên EMF = 90 độ nên tam giác MEF vuông tại M

a: ΔNEM cân tại N
nên góc NME=góc NEM
=>góc xME=góc nME
=>ME là phân giác của góc xMN
ΔNMF cân tại N
=>góc NMF=góc NFM
=>góc NMF=góc x'MF
=>MF là phân giác của góc x'MN
b: Xet ΔMEF có
MN là trung tuyến
MN=EF/2
Do đó: ΔMEF vuông tại M

a, Ta có: At∩xx′={A}(gt)At∩xx′={A}(gt)
Mà xx' // yy' (gt)
=> At ∩∩ yy' (hệ quả của tiên đề ơ-clit)
b,Tia At là phân giác góc xAB (gt)
=> góc xAt = góc BAt = Góc xAB / 2 = 80o/2 = 40o
Có: xx' // yy' (gt)
mà At ∩∩ yy' = {C} (gt)
=> Góc xAt = góc ACB = 40o (cặp góc so le trong )

mik quên viết hình mà các bạn thử đoán hình giúp mik với ạ

Lời giải
e) Từ các câu trên ta có nhận xét: tập hợp tất cả các điểm cách đều hai đường thẳng cắt nhau xx', yy' là các đường phân giác tạo bởi các góc của hai đường thẳng đó.
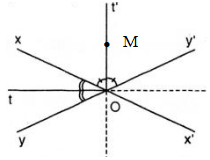


a: ΔNME cân tại N
nên góc NEM=góc NME
=>góc NME=góc xME
=>ME là phân giác của góc xMN
ΔNMF cân tại N
nên góc NMF=góc NFM
=>góc NMF=góc xMF
=><MF là phân giác của góc xMN
b: Xét ΔMEF có
MN là trung tuyến
MN=EF/2
Do đó;ΔMEF vuông tại M