Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Đúng
b) Sai. Vì hai đường thẳng không cắt nhau có thể song song hoặc trùng nhau.
c) Đúng
d) Đúng
e) Đúng
f) Đúng

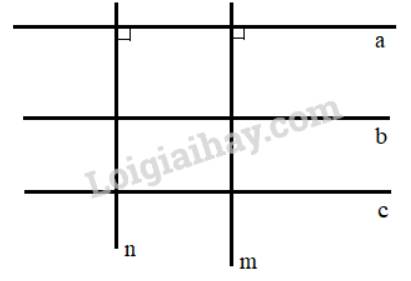
Ta có: +) a // b, b // c nên a // c ( Hai đường thẳng cùng song song với đường thẳng thứ ba thì chúng song song với nhau)
+) m \( \bot \) a; n \( \bot \)a nên m // n (Hai đường thẳng cùng vuông góc với một đường thẳng thứ ba thì song song với nhau)
Theo định lý “Đường thẳng vuông góc với 1 trong 2 đường thẳng song song thì cũng vuông góc với đường thẳng kia, ta có:
+) a // b; a \( \bot \)n nên b \( \bot \)n
+) a // b; a \( \bot \)m nên b \( \bot \)m
+) a // c; a \( \bot \)n nên c \( \bot \)n
+) a // c; a \( \bot \)m nên c \( \bot \)m
Vậy các cặp đường thẳng song song là: a // b ; a // c ; b // c; m // n
Các cặp đường thẳng vuôn góc là: b \( \bot \)n; b \( \bot \)m; c \( \bot \)n; c \( \bot \)m; a \( \bot \)n; a \( \bot \)m
đáp án 54 đường thẳng
Đáp án là 54 nha bạn!!!!