Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

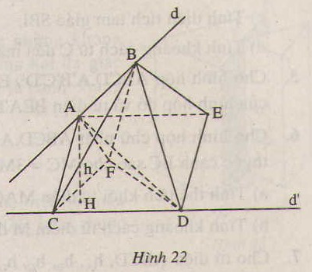
Gọi h là độ dài đường vuông góc chung của d và d’, α là góc giữa hai đường thẳng d và d’. Qua B, A, C dựng hình bình hành BACF. Qua A,C, D dựng hình bình hành ACDE.
Khi đó CFD.ABE là một hình lăng trụ tam giác. Ta có:
VDABC=VDFCB=VBCDF
= VCFD.ABE
= hSFCD=
h.
ab. sinα
=h. ab. sinα (là một số không đổi).
Xem thêm tại: http://loigiaihay.com/cau-6-trang-26-sgk-hinh-hoc-12-c47a2782.html#ixzz4cxsiVwHA

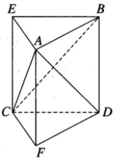
Dựng BE song song và bằng DC, DF song song và bằng BA. Khi đó, ABE.FDC là một lăng trụ đứng.
Ta có:
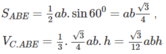
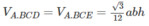

Đáp án B
Cách giải:
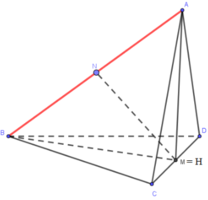
Gọi M là trung điểm của CD. Kẻ AH vuông góc mặt phẳng (BCD) (H thuộc (BCD)) ⇒ H ∈ BM, AH ⊥ HM
VABCD lớn nhất khi và chỉ khi AH có độ dài lớn nhất, tức là khi H trùng M
Hai tam giác ACD, BCD đều, cạnh a, có đường cao AM, BM bằng a 3 2
Tam giác ABM vuông cân tại A, lấy N là trung điểm của AB ⇒ MN ⊥ AB
Mà MN ⊂ (AMB) ⊥ CD ⇒ MN ⊥ CD ⇒ MN là đoạn vuông góc chung của AB và CD
Khoảng cách giữa hai đường thẳng AB và CD là:
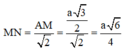

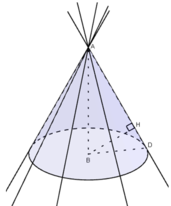
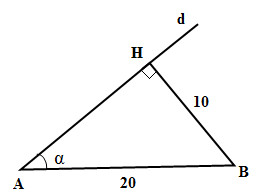
Từ B vẽ đường thẳng vuông góc với d và cắt d tại H.
Ta có BH = 10cm = d(B,d)
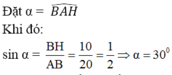
Vậy đường thẳng d nằm trên mặt nón có đỉnh là A, trục là đường thẳng AB và góc ở đỉnh là 2α = 60 °

Chọn B
Ta có d₁ đi qua điểm M (1;2;-3) và có vtcp ![]()
Đường thẳng d₂ đi qua điểm N (4;3;1) và có vtcp ![]()
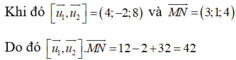
nên hai đường thẳng đã cho luôn chéo nhau và
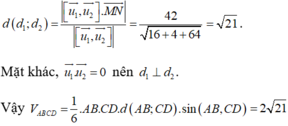


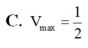
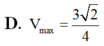
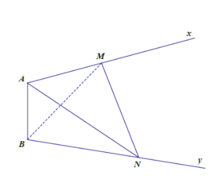

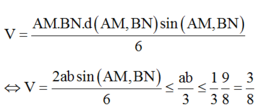
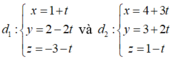

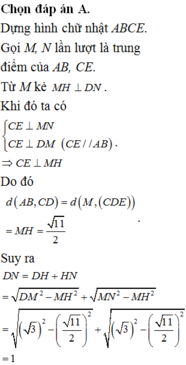


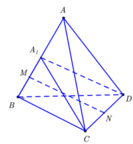
Gọi h là khoảng cách hai đường thẳng d và d’, gọi α là góc tạo bởi hai đường thẳng d và d’.
Lần lượt vẽ hai hình bình hành BACF và ACDE.
Khi đó, ABE.CFD là hình lăng trụ tam tam giác có chiều cao h; AE = CD = b và
Gọi S là diện tích đáy của hình lăng trụ .
Ta chia hình lăng trụ ABE. CFD thành ba hình chóp tam giác là: D. ABE, B. CFD, D.ABC. Ta có:
Do đó, thể tích khối tứ diện ABCD không đổi.