Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a. AM là phân giác của tam giác ABC cân tại A => AM cũng là đường cao và đường phân giác trong ta giác ABC
=> góc EAM = góc FAM
=> Tam giác EAM = tam giác FAM (cạnh huyền - góc nhọn)
=> EA=FA và EM = FM (1)
TA có: AB =AC => AB - AE = AC - ÀF <=> BE = FC (2)
Và AM là đường trung tuyến của tam giác ABC => BM =MC (3)
Từ (1), (2), (3) => tam giác BEM = tam giác CFM (c-c-c)
A E B F C D M
a, Xét t/g BEM và t/g CFM có:
góc BEM = góc CFM = 90 độ (gt)
MB = MC (gt)
góc B = góc C (gt)
=> t/g BEM = t/g CFM (cạnh huyền - góc nhọn)
b, Xét t/g AEM và t/g AFM có:
EM = FM (t/g BEM = t/g CFM)
góc AEM = góc AFM = 90 độ (gt)
AM chung
=> t/g AEM = t/ AFM (c.g.c)
=> AE = AF
=> tg/ AEF cân tại A
Mà AM là tia phân giác của t/g AEF
=> AM là đường trung trực của t/g AEF hay AM là đường trung trực của EF
c, Vì t.g ABC cân tại A và AM là trung tuyến cuả BC
=> AM cũng là đường trung trực của BC (1)
=> góc AMB = 90 độ
Xét t/g DMB và t/g DMC có:
MB = MC (gt)
góc DMB = góc DMC = 90 độ (cmt)
DM chung
=> t/g DMB = t/g DMC (c.g.c)
=> DB = DC => D thuộc trung trực của BC
Mà MB = MC => M thuộc trung trực của BC
=> DM là trung trực của BC (2)
Từ (1) và (2) => A,D,M thẳng hàng

Bạn tham khảo tại đây:
Câu hỏi của KHÔNG CẦN BIẾT - Toán lớp 7 - Học toán với OnlineMath

A B C M O I
a, xét tam giác BCO và tam giác CBI có : BC chung
góc BOC = góc CIB = 90 (Gt)
tam giác ABC cân tại A và BI; CO là đường cao => BI = CO (tc)
=> tam giác BCO = tam giác CBI (ch-cgv)
=> góc BCO = góc CBI (đn)
có góc BCO + góc OCA = góc ACB
góc CBI + góc IBA = góc ABC
góc ABC = góc ACB do tam giác ABC cân tại A (gt)
=> góc IBA = góc OCA
xét tam giác ABM và tam giác ACM có : AB = AC (tam giác ABC cân tại A)
BM = MC
=> tam giác ABM = tam giác ACM

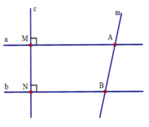
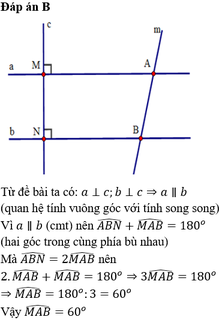
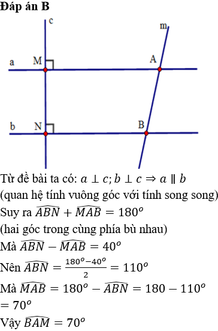
Từ đề bài ta có: a ⊥ c, b ⊥ c ⇒ a // b (quan hệ từ vuông góc đến song song)
⇒ ∠ABN + ∠MAB = 180° (hai góc trong cùng phía bù nhau)
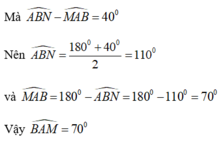
Chọn đáp án B.