Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn đáp án C
Lấy điểm M trên a, qua M kẻ đường thẳng b' song song với b. Khi đó mặt phẳng (a;b') song song với b.
Nếu có một mặt phẳng (P) khác (a;b') chứa a mà song song với b khi đó P ∩ a ; b ' = a phải song song với b. Mâu thuẩn a, b chéo nhau. Vậy có duy nhất một mặt phẳng chứa a và song song với b.

Đáp án C
Mệnh đề 1 đúng.
Mệnh đề 2 sai vì 2 đường thẳng đó có thể chéo nhau.
Mệnh đề 3 sai vì 2 đường thẳng đó có thể song song.
Mệnh đề 4 sai

Đáp án D
a và b chéo nhau. Có duy nhất một mặt phẳng chứa a và song song với b vì có duy nhất một mặt phẳng chứa hai đường thẳng cắt nhau.

Đáp án D
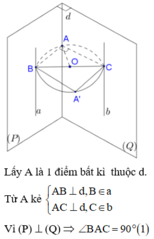
Ta đi chứng minh BC chính là khoảng cách giữa hai đường thẳng a và b, BC = 4:
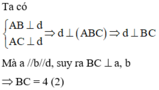
Từ (1) (2) suy ra A thuộc đường tròn đường kính BC bằng 4 không đổi
Do đó d thuộc mặt trụ có khoảng cách giữa đường sinh và trục bằng 2



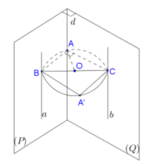
Đáp án D
Chỉ có duy nhất cặp mặt phẳng như vậy