Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Vì q1 và q2 trái dấu nên để cặp lực do q1 và q2 tác dụng lên q0 là cặp lực trực đối (\(\overrightarrow{F_{10}}\) \(=-\overrightarrow{F_{20}}\)) thì q0 phải nằm trên đường thẳng AB và gần A hơn (do |q1| < |q2|).
Gọi x (m) là khoảng cách từ q1 đến q0, ta có: F10 = F20
⇔ \(\frac{k.\left|q_1.q_0\right|}{x^2}=\frac{k.\left|q_2.q_0\right|}{\left(AB+x\right)^2}\) ⇒ 2.10-8.(6,4.10-3 + 0,16x + x2) = 1,8.10-7.x2
⇔ -1,6.10-7.x2 + 3,2.10-9.x + 1,28.10-10 = 0
⇔ x = 0,04 (m)
Vậy để q0 cân bằng thì phải đặt q1 cách A 4 cm.
b) Điều kiện để q1 và q2 cũng cân bằng: q0 cách q1 4 cm, cặp lực do q0 và q2 tác dụng lên q1 phải là cặp lực trực đối, đồng thời cặp lực do q1 và q0 tác dụng lên q2 cũng là cặp lực trực đối. Để thỏa mãn điều kiện đó thì q0 phải cùng dấu với q1 và:
F10 = F12 ⇔ \(\frac{k.\left|q_1.q_0\right|}{x^2}=\frac{k.\left|q_1.q_2\right|}{AB^2}\) ⇔ \(\frac{9.10^9.\left|-2.10^{-8}.q_0\right|}{0,04^2}=\frac{9.10^9.\left|-2.10^{-8}.1,8.10^{-7}\right|}{0,08^2}\)
⇒ q0 = \(-4,5.10^{-8}\) (C)
Vậy q0 = \(-4,5.10^{-8}\) (C) để q1 và q2 cũng cân bằng.


Để hệ 3 điện tích cân bằng thì lực điện tác dụng lên 2 điện tích bắt kì tác dụng lên điện tích còn lại phải bằng 0.
Để q3 cân bằng thì F23=F13 = \(\dfrac{k\left|q_1q_3\right|}{r^2_{1^{ }}}=\dfrac{k\left|q_2q_3\right|}{r^2_2}\left(1\right)\)
=> Điện tích q3 mang dấu âm, nằm ngoài khoảng q1,q2 và gần q1 hơn (Vì nằm gần vị trí điện tích có độ lớn lớn hơn)
Từ (1) => \(\dfrac{r1}{r2}=\sqrt{\dfrac{q1}{q2}}=\dfrac{1}{3}\)
Có: r2 - r1 =12 => r1=6 cm, r2=18 cm.
Để q1 cân bằng thì F31 = F21 khai triển và thay số ta được : q3 = -4,5.10-8 C.

a) Các điện tích q 1 v à q 2 tác dụng lên điện tích q 3 các lực điện F 13 → và F 23 → .
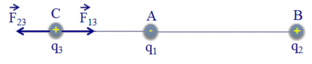
Để q 3 nằm cân bằng thì F 13 → + F 23 → = 0 → ð F 13 → = - F 23 → ð F 13 → và F 23 → phải cùng phương, ngược điều và bằng nhau về độ lớn. Để thoả mãn điều kiện đó thì C phải nằm trên đường thẳng nối A, B (để F 13 → và F 23 → cùng phương), nằm ngoài đoạn thẳng AB (vì q 1 v à q 2 trái dấu, q 3 có thể là điện tích dương hay âm đều được, trong hình q 3 là điện tích dương) và gần A hơn (vì q 1 < q 2 ).
Khi đó: k | q 1 q 3 | A C 2 = k | q 2 q 3 | ( A B + A C ) 2 ð A B + A C A C = | q 2 | | q 1 | = 3
⇒ AC = 4 cm; BC = 12 cm.
b) Để q 1 v à q 2 cũng cân bằng thì:
F 21 → + F 31 → = 0 → và F 12 → + F 32 → = 0 → ð F 21 → = - F 31 → và F 12 → = - F 32 → .
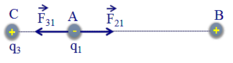
Để F 21 → và F 31 → ngược chiều thì q 3 > 0 và k | q 3 q 1 | A C 2 = k | q 2 q 1 | A B 2
⇒ q 3 = q 2 A C A B 2 = 0 , 45 . 10 - 6 C .
Vậy q 3 = 0 , 45 . 10 - 6 C.

Chọn đáp án A
Để hệ 3 điện tích cân bằng thì lực điện do 2 điện tích bất kì tác dụng lên điện tích còn lại phải bằng 0
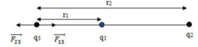



Điện tích q 1 tác dụng lên q 0 lực F 1 → , điện tích q2 tác dụng lên q 0 lực F 2 → .
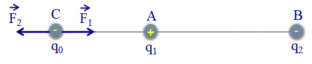
Để q0 nằm cân bằng thì F 1 → + F 2 → = 0 → ð F 1 → = - F 2 → ð F 1 → và F 2 → phải cùng phương, ngược chiều và bằng nhau về độ lớn. Để thỏa mãn các điều kiện này thì q0 phải đặt trên đường thẳng nối A, B (để hai lực cùng phương), đặt ngoài đoạn thẳng AB (để hai lực ngược chiều) và gần q1 hơn (để hai lực bằng nhau về độ lớn vì | q 1 | < | q 2 |).
Khi đó: k | q 1 q 0 | A C 2 = k | q 2 q 0 | ( A B + A C ) 2 ⇒ A B + A C A C = | q 2 | | q 1 | = 2
⇒ AC = 20 cm; BC = BA + AC = 40 cm.

![]()
Giả sử q 0 > 0. Để q0 cân bằng thì hợp lực tác dụng lên q 0 phải bằng không, ta có:
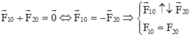
Vì q1; q2 cùng dấu nên C thuộc đoạn thẳng AB: AC + BC = AB (*) và q 1 A C 2 = q 2 B C 2 (**)
Từ (*) và (**) ta có:
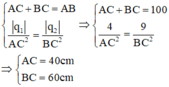

Nếu giá trị q1 và q2 như vậy thì đề bài không có đáp án, khi đó q3 cách q1 4cm và cách q2 12 cm.
Nếu đề bài có giá trị \(\left\{{}\begin{matrix}q_1=-2\cdot10^{-8}C\\q_2=-1,8\cdot10^{-7}C\end{matrix}\right.\) thì đề bài có đáp án và chọn A khi đó.
Mình giải theo đề bài đã sửa:
\(q_1,q_2\) cùng dấu\(\Rightarrow q_1,q_2\) nằm trên đường nối hai điện tích.
q3 cân bằng khi: \(F_1=F_2\)
\(\Rightarrow\dfrac{\left|q_1\right|}{r^2_1}=\dfrac{\left|q_2\right|}{r^2_2}\)\(\Rightarrow\dfrac{2}{r^2_1}=\dfrac{1,8}{r^2_2}\)\(\Rightarrow3r_1=r_2\) (1)
Mặt khác: \(r_1+r_2=0,08\) (2)
Từ (1) và (2) \(\Rightarrow\left\{{}\begin{matrix}r_1=0,02m=2cm\\r_2=0,06m=6cm\end{matrix}\right.\)
