Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

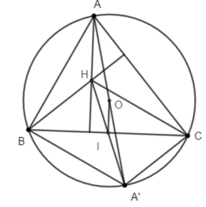
Gọi A’ là điểm đối xứng với A qua O. Ta có: BH // A’C suy ra BHCA’ là hình bình hành do đó HA’ cắt BC tại trung điểm I của BC. Mà O là trung điểm của AA’ suy ra OI là đường trung bình của tam giác AHA’ suy ra A H → = 2 O I →
Chọn đáp án C

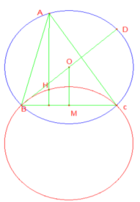
- Kẻ đường kính BB’
.Nếu H là trực tâm của tam giác ABC thì AH=B’C. Do C,B’ cố định , cho nên B’C là một véc tơ cố định => AH = B'C
. Theo định nghĩa về phép tịnh tiến điểm A đã biến thành điểm H .
Nhưng A lại chạy trên (O;R) cho nên H chạy trên đường tròn (O’;R) là ảnh của (O;R) qua phép tịnh tiến dọc theo v = B'C
- Cách xác định đường tròn (O’;R) .
Từ O kẻ đường thẳng song song với B’C . Sau đó dựng véc tơ : OO' = B'C
Cuối cùng từ O’ quay đường tròn bán kính R từ tâm O’ ta được đường tròn cần tìm .

Bạn lấy thực hiện phép đối xứng qua \(BC\) thì \(O\) thành \(O'\) thì \(OB=O'B,OC=O'C\) mà \(OB=C=R\) cho nên \(O'B=O'C=R\left(1\right)\)
Ở đây \(R\) là bán kính đường tròn ngoại tiếp \(ABC'\)
, \(H\) thành \(H'\) với \(O\) là tâm đường tròn ngoại tiếp \(ABC\).
Cho nên \(\widehat{HBC}=\widehat{H'BC}\) ( phép đối xứng trực bảo toàn góc) mặt khác
\(\widehat{HBC}=\widehat{HAC}\) cùng phụ với góc \(\widehat{C}\).
Điều này chứng tỏ \(ACH'B\) là tứ giác nội tiếp hay \(H'\) cũng thuộc \(\left(O\right)\)
Phép đối xứng là phép dời hình cho nên nó bảo toàn khoảng cách cũng có nghĩa
\(O'H=OH'=R\) (vì \(H\) nằm trên \(\left(O\right)\)) (2)
Từ (1) và (2) ta được tam giác HBC luôn nội tiếp đường tròn \(\left(O'\right)\) bán kính R
do \(O,BC\) và R cố định nên \(O'\) cố định , ta được điều phải chứng minh.

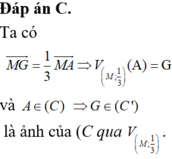
Đáp án D
Gọi BB’ là đường kính (O).
T B ' C → : O → O ' ⇒ O O ' / / B ' C (1)
Ta lại có
B’C // AH ( cùng vuông góc BC) (2)
B’A // CH ( cùng vuông góc BA)
AH = B’C (3)
Từ (1), (2), (3): O O ' / / A H O O ' = A H =>O’H = OA = R
=> H ∈ (O’,R)