Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi M là trung điểm của AB, ta có \(M=\left(\frac{3}{2};\frac{1}{2};-\frac{1}{2}\right)\)
Vì (P) là mặt phẳng trung trực của AB nên (P) đi qua M và \(\overrightarrow{AB}=\left(-1;1;-1\right)\) là một vecto pháp tuyến của (P)
Suy ra, phương trình của (P) là : \(\left(-1\right)\left(x-\frac{3}{2}\right)+\left(y-\frac{1}{2}\right)+\left(-1\right)\left(z+\frac{1}{2}\right)=0\)
hay : \(2x-2y+2z-1=0\)
Ta có : \(d\left(O,\left(P\right)\right)=\frac{\left|-1\right|}{\sqrt{2^2+\left(-2\right)^2+2^2}}=\frac{1}{2\sqrt{3}}\)
Do đó phương trình mặt cầu tâm O , tiếp xúc với (P) là \(x^2+y^2+z^2=\frac{1}{12}\)
hay : \(12x^2+12y^2+12z^2-1=0\)

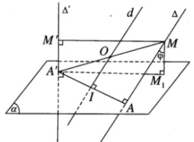
Theo giả thiết ta có: ∠A′M′M = ∠A′AM = ∠A′M1M = 90o
Do đó 5 điểm A, A’, M, M’, M1 cùng thuộc mặt cầu (S) tâm O, với O là trung điểm của A’M và có bán kính r = A′M2
Mặt khác ta có A’M2 = A’A2 + AM2
Trong đó
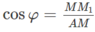
Do đó
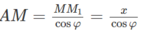
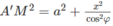
Mặt cầu tâm O có bán kính
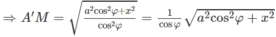
Diện tích của mặt cầu tâm O là:
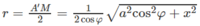

Chọn A.
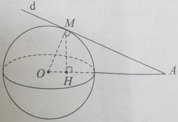
Trong mặt phẳng (d,O), tam giác OMA vuông tại M có MH là đường cao nên:
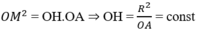
⇒ H cố định
Vậy M thuộc mặt phẳng vuông góc với OA tại H.

Đáp án A
Mặt phẳng (P) đi qua trung điểm I của đoạn thẳng AB và vuông góc với AB.


Hai mặt phẳng (SAB) và (SAC) cùng vuông góc với (ABC) \(\Rightarrow SA\perp\left(ABC\right)\)
\(AB\perp BC\Rightarrow SB\perp BC\Rightarrow\widehat{SBA}\) là góc giữa 2 mặt phẳng (SBC) và mặt phẳng (ABC)
\(\Rightarrow\widehat{SBA}=60^o\)
\(\Rightarrow SA=AB.\tan\widehat{SBA}=2a\sqrt{3}\)
Mặt phẳng qua SM và song song với BC, cắt AC tại N
\(\Rightarrow MN||BC\) và N là trung điểm của \(AC\\ \)
\(MN=\frac{BC}{2}=a;BM=\frac{AB}{2}=a\)
Diện tích \(S_{BCNM}=\frac{\left(BC+MN\right).BM}{2}=\frac{3a^2}{2}\)
Thể tích \(V_{S.BCNM}=\frac{1}{3}S_{BCNM}.SA=a^3\sqrt{3}\)
Kẻ đường thẳng \(\Delta\) đi qua N, song song với AB
Hạ \(AD\perp\Delta\left(D\in\Delta\right)\Rightarrow AB||\left(SND\right)\)
\(\Rightarrow d\left(AB;SN\right)=d\left(AB,\left(SND\right)\right)=d\left(A,\left(SND\right)\right)\)
Hạ \(AH\perp SD\left(H\in SD\right)\Rightarrow AH\perp\left(SND\right)\Rightarrow d\left(A,\left(SND\right)\right)=AH\)
Tam giác SAD vuông tại A : \(\begin{cases}AH\perp SD\\AD=MN=a\end{cases}\)
\(\Rightarrow d\left(AB,SN\right)=AH=\frac{SA.AD}{\sqrt{SA^2+AD^2}}=\frac{2a\sqrt{39}}{13}\)
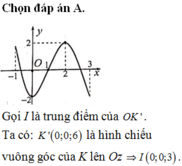

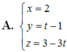
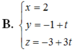
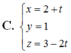
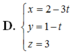

Chọn A.
Gọi I là tâm mặt cầu đi qua hai điểm A, B cố định và phân biệt thì ta luôn có IA = IB. Do đó I thuộc mặt phẳng trung trực của đoạn AB.