Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(P(x) + Q(x) = - 3{x^4} - 8{x^2} + 2x + 5{x^3} - 3{x^2} + 4x - 6\)
\( = - 3{x^4} + 5{x^3} + ( - 8{x^2} - 3{x^2}) + (2x + 4x) - 6\)
\( = - 3{x^4} + 5{x^3} - 11{x^2} + 6x - 6\)
\(P(x) - Q(x) = - 3{x^4} - 8{x^2} + 2x - 5{x^3} + 3{x^2} - 4x + 6\)
\( = - 3{x^4} - 5{x^3} + ( - 8{x^2} + 3{x^2}) + (2x - 4x) + 6\)
\( = - 3{x^4} - 5{x^3} - 5{x^2} - 2x + 6\)

Tham khảo:
Cách 1 :
Ta có P(x) - Q(x)
= 2x3 – 9x2 + 5 – (2x2 + 4x3 – 7x)
= 2x3 – 9x2 + 5 – 2x2 – 4x3 + 7x
= (2x3 – 4x3) + (-9x2 – 2x2) + 7x + 5
= -2x3 – 11x2 + 7x + 5
Cách 2 :
P(x) = 2x3 – 9x2 + 5
Q(x) = 4x3 + 2x2 – 7x
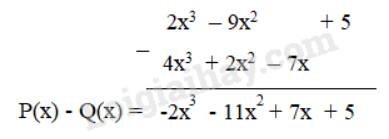

P(x)+Q(x)+R(x) = \(9{x^4} - 3{x^3} + 5x - 1 - 2{x^3} - 5{x^2} + 3x - 8 - 2{x^4} + 4{x^2} + 2x - 10\)
\(\begin{array}{l} = (9{x^4} - 2{x^4})+( - 3{x^3} - 2{x^3})+( - 5{x^2} + 4{x^2}) +( 5x + 3x + 2x)+( - 8 - 10 - 1)\\ = 7{x^4} - 5{x^3} - {x^2} + 10x - 19\end{array}\)
P(x)-Q(x)-R(x) = \(9{x^4} - 3{x^3} + 5x - 1 + 2{x^3} + 5{x^2} - 3x + 8 + 2{x^4} - 4{x^2} - 2x + 10\)
\(\begin{array}{l} = (9{x^4} + 2{x^4})+( - 3{x^3} + 2{x^3} )+ (5{x^2} - 4{x^2}) + (5x - 3x - 2x) + (10 - 1 + 8)\\ = 11{x^4} - {x^3} + {x^2} + 17\end{array}\)

P(x)=-5x^3-1/3+8x^4+x^2
Q(x)=x^4-2x^3+x^2-5x-2/3
P(x)+Q(x)
=x^4-2x^3+x^2-5x-2/3+8x^4-5x^3+x^2-1/3
=9x^4-7x^3+2x^2-5x-1
P(x)-Q(x)
=x^4-2x^3+x^2-5x-2/3-8x^4+5x^3-x^2+1/3
=-7x^4+3x^3-5x-1/3

\(P\left(x\right)+Q\left(x\right)=\left(2x^4+x^3-4x+5\right)+\left(x^4+3x^3+2x-1\right)\)
\(=2x^4+x^3-4x+5+x^4+3x^3+2x-1\)
\(=\left(2x^4+x^4\right)+\left(x^3+3x^3\right)+\left(-4x+2x\right)+\left(5-1\right)\)
\(=3x^4+4x^3-2x+4\)
\(R\left(x\right)+P\left(x\right)=x^4-2x^2+1\)
\(\Rightarrow R\left(x\right)=\left(x^4-2x^2+1\right)-P\left(x\right)\)
\(\Rightarrow R\left(x\right)=\left(x^4-2x^2+1\right)-\left(2x^4+x^3-4x+5\right)\)
\(\Rightarrow R\left(x\right)=x^4-2x^2+1-2x^4-x^3+4x-5\)
\(\Rightarrow R\left(x\right)=\left(x^4-2x^4\right)+\left(-2x^2\right)+\left(1-5\right)+\left(-x^3\right)+4x\)
\(\Rightarrow R\left(x\right)=-x^4-2x^2-4-x^3+4x\)

a) Bậc P(x) = 4 + 3 + 1 = 8
Bậc của Q (x) = 2 + 3 + 1 = 6
b) P(x) + Q ( x) = x4 + x3 -2x + 1 + 2x2 -2x3 + x- 5
= x4 -x3 + 2x2 -x - 4
P(x) - Q (x) = x4 +x3 -2x + 1 - 2x2 -2x3 + x - 5
= x4 + 3x 3 -2x2 - 3x + 6
a) Bậc của đa thức P(x) là: 4+3+1=8
Bậc xủa đa thức Q(x) là: 2+3+1=6
b) P(x)+Q(x)=(x4+x3-2x+1)+(2x2-2x3+x-5)
P(x)+Q(x)=x4+x3-2x+1+2x2-2x3+x-5
P(x)+Q(x)=x4-x3+2x2-x-4
P(x)-Q(x)=(x4+x3-2x+1)-(2x2-2x3+x-5)
P(x)-Q(x)=x4+x3-2x+1-2x2+2x3-x+5
P(x)-Q(x)=x4+3x3-2x2-3x+6

Tham khảo:
Cách 1:
P(x) + Q(x) = \(7{x^3} - 8x + 12 + 6{x^2} - 2{x^3} + 3x - 5\)
\(\begin{array}{l} = (7{x^3} - 2{x^3}) + 6{x^2} + ( - 8x + 3x) + (12 - 5)\\ = 5{x^3} + 6{x^2} - 5x + 7\end{array}\)
Cách 2:
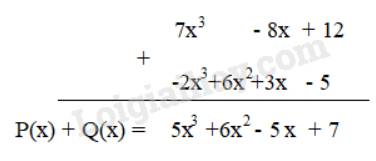
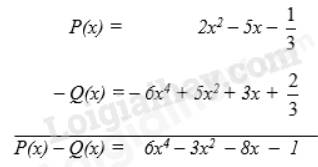
Sắp xếp hai đa thức theo lũy thừa giảm dần của biến rồi sau đó thực hiện phép tính: