Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) f(x) = 10x² - 7x - 5 = 10x² - 15x + 8x - 12 + 7 = 5x(2x-3) + 4(2x-3) + 7
f(x) chia hết cho 2x-3 khi và chỉ khi 7 chia hết cho 2x-3, vì 7 là số nguyên tố, nên chi có các trường hợp:
TH1: 2x-3 = -1 <=> x = 1
TH2: 2x-3 = 1 <=> x = 2
TH3: 2x-3 = -7 <=> x = -2
TH4: 2x-3 = 7 <=> x = 5
Vây có 4 giá trị nguyên của x là {-2, 1, 2, 5}
a) f(x) = 10x² - 7x - 5 = 10x² - 15x + 8x - 12 + 7 = 5x(2x-3) + 4(2x-3) + 7
f(x) chia hết cho 2x-3 khi và chỉ khi 7 chia hết cho 2x-3, vì 7 là số nguyên tố, nên chi có các trường hợp:
TH1: 2x-3 = -1 <=> x = 1
TH2: 2x-3 = 1 <=> x = 2
TH3: 2x-3 = -7 <=> x = -2
TH4: 2x-3 = 7 <=> x = 5
Vây có 4 giá trị nguyên của x là {-2, 1, 2, 5}
b) g(x) = x³ - 4x² + 5x - 1 = x³ - 3x² - x² + 3x + 2x - 6 + 5 = x²(x-3) - x(x-3) + 2(x-3) + 5
g(x) chia hết cho x-3 khi và chỉ khi 5 chia hết cho x-3 (5 là số nguyên tố nên chỉ xét các trường hợp)
TH1: x-3 = -5 <=> x = -2
TH2: x-3 = -1 <=> x = 2
TH3: x-3 = 1 <=> x = 4
TH4: x-3 = 5 <=> x = 8
Vậy có giá trị nguyên của x thỏa là {-1, 2, 4, 8}

Bài 1:
(x² - 8)(x³ + 2x + 4)
= x².x³ + x².2x + x².4 - 8.x³ - 8.2x - 8.4
= x⁵ + 2x³ + 4x² - 8x³ - 16x - 32
= x⁵ - 6x³ + 4x² - 16x - 32
Bài 2
a) A(x) = -5/3 x² + 3/4 x⁴ + 2x - 7/3 x² - 2 + 4x + 1/4 x⁴
= (3/4 x⁴ + 1/4 x⁴) + (-5/3 x² - 7/3 x²) + (2x + 4x) - 2
= x⁴ - 4x² + 6x - 2
b) Bậc của A(x) là 4
Hệ số cao nhất là 1

Lời giải:
a.
$A+B=(5x^2-7x+2)+(4x^2+3x-1)=9x^2-4x+1$
$A-B=(5x^2-7x+2)-(4x^2+3x-1)=x^2-10x+3$
b.
$A(x)=2x^2-x+m=x(2x-5)+4x+m=x(2x-5)+2(2x-5)+m+10$
$=B(x)(x+2)+m+10$
Để $A(x)\vdots B(x)$ thì $m+10=0\Leftrightarrow m=-10$

Mình xp giúp được mỗi câu đầu thôi nha ;-;;;; 2 câu sau mình chưa học, bạn thông cảm ;-;;;.
`a,` \(\text{P(x) =}\)\(2x^3-3x+x^5-4x^3+4x-x^5+x^2-2\)
`P(x)= (2x^3 - 4x^3)-(3x-4x) +(x^5-x^5) +x^2-2`
`P(x)= -2x^3- (-x)+0+x^2-2`
`P(x)=-2x^3+x+x^2-2`
`Q(x)= x^3-x^2+3x+1+3x^2`
`Q(x)= x^3- (x^2-3x^2) +3x+1`
`Q(x)=x^3- (-2x^2)+3x+1`

Lời giải:
$2x^3-4x^2+a-10=2x^2(x-2)+a-10$
$\Rightarrow$ để $2x^3-4x^2+a-10$ chia hết cho $x-2$ thì $a-10=0$
$\Leftrightarrow a=10$

a)
\(\begin{array}{l}(3x - 1) + \left[ {(2{x^2} + 5x) + (4 - 3x)} \right] = 3x - 1 + 2{x^2} + 5x + 4 - 3x\\ = 2{x^2}+( 3x +5x- 3x )+ (4 - 1) = 2{x^2} + 5x + 3\end{array}\)
b) Vì A + B = C nên B = C – A
Ta được: B = \(5 - 3{x^2} - 4x - 2\)
\( = - 3{x^2} - 4x + 3\)
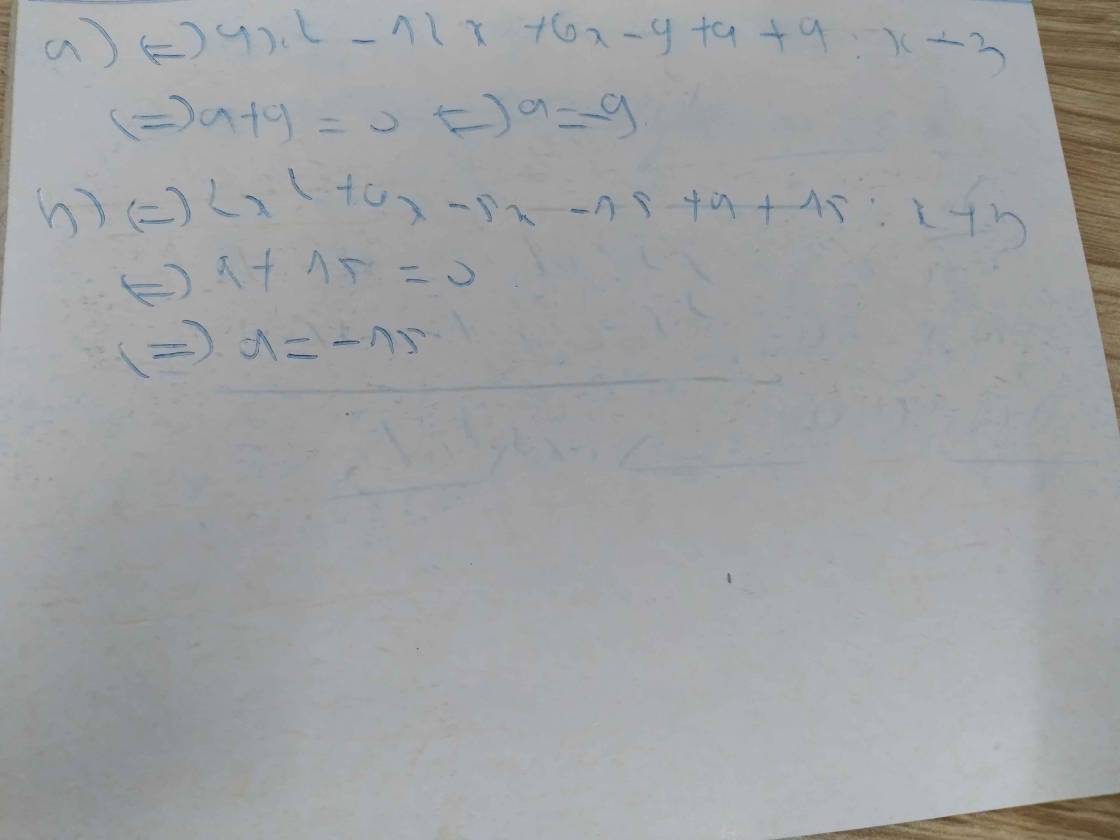
a: \(\dfrac{A}{B}=\dfrac{x^3+4x^2+3x+12-19}{x+4}=x^2+3+\dfrac{-19}{x+4}\)
b: Để A chia hết cho B thì \(x+4\in\left\{1;-1;19;-19\right\}\)
=>\(x\in\left\{-3;-5;15;-23\right\}\)