Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Câu hỏi của nguyenvandat - Toán lớp 7 - Học toán với OnlineMath

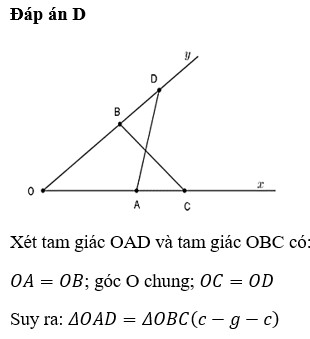
a: Xét ΔOAD và ΔOCB có
OA=OC
\(\widehat{AOD}\) chung
OD=OB
Do đó: ΔOAD=ΔOCB
b: Xét ΔOBD có \(\dfrac{OA}{OB}=\dfrac{OC}{OD}\)
nên AC//BD
c: Ta có: ΔOAD=ΔOCB
=>\(\widehat{OAD}=\widehat{OCB};\widehat{ODA}=\widehat{OBC}\)
Ta có: \(\widehat{OAD}+\widehat{DAB}=180^0\)(hai góc kề bù)
\(\widehat{OCB}+\widehat{DCB}=180^0\)(hai góc kề bù)
mà \(\widehat{OAD}=\widehat{OCB}\)
nên \(\widehat{DAB}=\widehat{DCB}\)
Ta có: OA+AB=OB
OC+CD=OD
mà OA=OC và OB=OD
nên AB=CD
Xét ΔMAB và ΔMCD có
\(\widehat{MAB}=\widehat{MCD}\)
AB=CD
\(\widehat{MBA}=\widehat{MDC}\)
Do đó: ΔMAB=ΔMCD
=>MB=MD
Xét ΔOMB và ΔOMD có
OM chung
MB=MD
OB=OD
Do đó: ΔOMB=ΔOMD
=>\(\widehat{BOM}=\widehat{DOM}\)
=>\(\widehat{xOM}=\widehat{yOM}\)
=>OM là phân giác của góc xOy
d: Ta có: OB=OD
=>O nằm trên đường trung trực của BD(1)
Ta có: MB=MD
=>M nằm trên đường trung trực của BD(2)
Ta có: NB=ND
=>N nằm trên đường trung trực của BD(3)
Từ (1),(2),(3) suy ra O,M,N thẳng hàng

Chohttps://olm.vn/cau-hoi/cho-goc-nhon-xoy-tren-canh-ox-lay-hai-diem-a-va-b-sao-cho-a-nam-giua-o-va-b-tren-canh-oy-lay-2-diem-c-va-d-sao-cho-c-nam-giua-o-va-d-cm-ab-c.5323815386517?lop=7

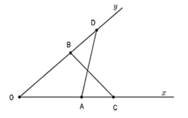
a: Xét ΔOAD và ΔOBC có
OA=OB
\(\widehat{O}\) chung
OD=OC
Do đó: ΔOAD=ΔOBC