Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Em tham khảo tại link dưới đây nhé.
Câu hỏi của trần thị thúy vân - Toán lớp 7 - Học toán với OnlineMath

a, Xét △OAM vuông tại A và △OBM vuông tại B
Có: AOM = BOM (gt)
OM là cạnh chung
=> △OAM = △OBM (ch-gn)
=> AM = BM (2 cạnh tương ứng)
và OA = OB (2 cạnh tương ứng)
=> △OAB cân tại O
b, Xét △MAD vuông tại A và △MBE vuông tại B
Có: AM = MB (cmt)
AMD = BME (2 góc đối đỉnh)
=> △MAD = △MBE (cgv-gnk)
=> MD = ME (2 cạnh tương ứng)
c, Gọi OM ∩ DE = { I }
Ta có: OA + AD = OD và OB + BE = OE
Mà OA = OB (cmt) , AD = BE (△MAD = △MBE)
=> OD = OE
Xét △IOD và △IOE
Có: OD = OE (cmt)
DOI = EOI (gt)
OI là cạnh chung
=> △IOD = △IOE (c.g.c)
=> OID = OIE (2 góc tương ứng)
Mà OID + OIE = 180o (2 góc kề bù)
=> OID = OIE = 180o : 2 = 90o
=> OI ⊥ DE
Mà OM ∩ DE = { I }
=> OM ⊥ DE

Em tham khảo tại link dưới đây nhé.
Câu hỏi của trần thị thúy vân - Toán lớp 7 - Học toán với OnlineMath


tự kẻ hình nha
a) vì M thuộc tia phân giác của xOy=> M cách đều Ox,Oy=> MA=MB
xét tam giác OBM và tam giác OAM có
OBM=OAM(=90 độ)
OM chung
BOM=AOM( gt)
=> tam giác OBM= tam giác OAM(ch-gnh)
=> OA=OB( hai cạnh tương ứng)
=> tam giác ABO cân O
b) vì M thuộc tia phân giác của góc xOy=>ME=MD
c) vì BD,AE,OM cùng giao nhau tại M
mà BD,AE là đường cao => OM là đường cao ( 3 đường cao cùng đi qua một điểm)
=> OM vuông góc với DE

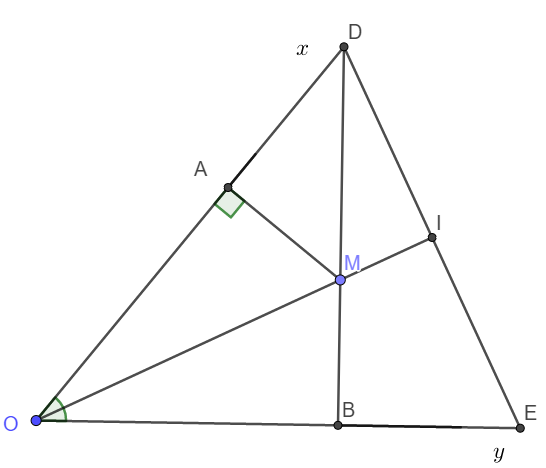
a) Xét tam giác vuông AOM và tam giác vuông BƠM có:
Cạnh huyền AM chung
\(\widehat{AOM}=\widehat{BOM}\) (gt)
\(\Rightarrow\Delta AOM=\Delta BOM\) (Cạnh huyền - góc nhọn)
\(\Rightarrow MA=MB;OA=AB\)hay tam giác OAB cân tại O.
b) Xét tam giác vuông AMD và tam giác vuông BME có:
AM = BM
\(\widehat{AMD}=\widehat{BME}\) (Hai góc đối đỉnh)
\(\Rightarrow\Delta AMD=\Delta BME\) (Cạnh góc vuông - góc nhọn kề)
\(\Rightarrow MD=ME\)
c) Ta thấy OA = OB; AD = BE nên OD = OE
Vậy thì \(\Delta ODI=\Delta OEI\left(c-g-c\right)\)
\(\Rightarrow\widehat{OID}=\widehat{OIE}\)
Chúng lại là hai góc kề bù nên \(\widehat{OID}=\widehat{OIE}=90^o\) hay MO vuông góc DE.
a: Xét ΔOAM vuông tại A và ΔOBM vuông tại B có
OM chung
\(\widehat{AOM}=\widehat{BOM}\)
Do đó: ΔOAM=ΔOBM
=>MA=MB
Xét ΔMAF vuông tại A và ΔMBE vuông tại B có
MA=MB
\(\widehat{AMF}=\widehat{BME}\)
Do đó: ΔMAF=ΔMBE
=>MF=ME
b:
Ta có: OA=OB
=>O nằm trên đường trung trực của BA(1)
Ta có: MA=MB
=>M nằm trên đường trung trực của BA(2)
Từ (1) và (2) suy ra OM là đường trung trực của BA
=>OM\(\perp\)BA