
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Xét tg AOM và tg BOM có:
OA=OB (gt)
Góc AOM=góc BOM ( vì Oz là p/g của góc xOy )
Chung cạnh OM
=> Tg AOM = tg BOM ( c.g.c )
=> Góc OMA = góc OMB ( 2 góc tương ứng )
Còn đây là hình:( hơi tệ nên bạn thông cảm nha! )
Xet tam giac AOM va tam giac BOM la:
OA=OB (gt)
OM la canh chung
goc AOM= goc BOM (vi OZ la phan giac goc xOy)
Do do: tam giac OAM= tam giac OBM( c-g-c )
=> goc OMA = goc OMB (hai goc tuong ung)
Hinh hoi xau mog bn thog cam.

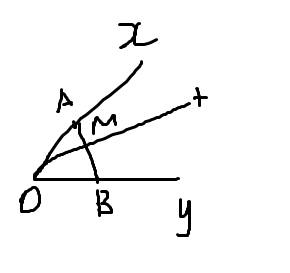
a. OA=OB
⇒ΔOAB cân tại O
mà OM là phân giác góc AOB
nên OM là đường trung tuyến ΔAOB
⇒M là trung điểm AB ⇒MA=MB
b. Xét ΔOAM và ΔOBM, có
OA=OB
OM chung
MA=MB
⇒ΔOAM = ΔOBM
nên OMA=OMB (đpcm)

a) xét tg OAH & tg OBH có :
OH chung
OA = OB ( gt )
góc AOH = góc BOH ( Ot p/g góc xOy )
suy ra tg OAH = tg OBH (c. g .c )
b) do tgOAH = tg OBH ( cmt )
suy ra góc OAH= góc OBH ( 2góc tg ứng )
Xét tg ONB & tg OAM có :
góc OAH= góc OBH ( cmt )
OA = OB ( gt )
góc O chung
suy ra tg ONB = tg OAM ( g . c .g )
c) có : OA = OB suy ra O thuộc trung trực AB (1)
tg tự có AH =BH ( 2 c tg ứng của tg OAH = tg OBH )
suy ra H thuộc trung trực OH (2)
từ (1) & (2) suy ra OH trung trực của AB
suy ra OH vuông góc AB
d) bn tự cm theo cách trên ( cm H thuộc trung trưc MN ) ![]()

a: Xét ΔADO và ΔBDO có
OA=OB
\(\widehat{AOD}=\widehat{BOD}\)
OD chung
Do đó: ΔADO=ΔBDO
b: Xét ΔOED vuông tại E và ΔOFD vuông tại F có
OD chung
\(\widehat{EOD}=\widehat{FOD}\)
Do đó: ΔOED=ΔOFD
Suy ra: OE=OF
c: Xét ΔOAB có
OE/OA=OF/OB
Do đó: EF//AB

Xét ΔCBD và ΔADB có
CD=AB
\(\widehat{CDB}=\widehat{ABD}\)
BD chung
Do đó: ΔCBD=ΔADB
Suy ra: \(\widehat{EBD}=\widehat{EDB}\)
hay ΔEBD cân tại E
Xét ΔOEB và ΔOED có
OE chung
EB=ED
OB=OD
Do đó: ΔOEB=ΔOED
Suy ra: \(\widehat{BOE}=\widehat{DOE}\)
hay OE là tia phân giác của góc xOy

Tham khảo:
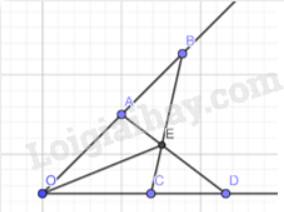
a) Xét \(\Delta OAD\) và \(\Delta OCB\), ta có :
OD = OB
\(\widehat{A}\) chung
OA = OC
\(\Rightarrow \Delta OAD=\Delta OCB\) (c-g-c )
\( \Rightarrow AD = BC\)(2 cạnh tương ứng )
b) Vì \(\Delta OAD=\Delta OCB\) nên \(\widehat{OAD}=\widehat{OCB}; \widehat{D}=\widehat{B}\) ( 2 góc tương ứng)
Mà \(\widehat{OAD}+\widehat{BAD}=180^0\) ( 2 góc kề bù)
\(\widehat{OCB}+\widehat{BCD}=180^0\) ( 2 góc kề bù)
Do đó, \(\widehat{BAD}=\widehat{BCD}\)
Vì \(OA+AB=OB; OC+CD=OD\)
Mà \(OC = OA, OD = OB\)
\(\Rightarrow AB=CD\)
Xét \(\Delta EAB\) và \(\Delta ECD\), ta có:
\(\widehat {ABE} = \widehat {CDE}\)
\(AB = CD\)
\(\widehat {BAE} = \widehat {DCE}\)
\(\Rightarrow \Delta EAB=\Delta ECD\) (g-c-g)
c) Vì \(\Delta EAB=\Delta ECD\) nên EB = ED ( 2 cạnh tương ứng)
Xét \(\Delta OBE\) và \(\Delta ODE\), ta có :
EB = ED
OB = OD
OE chung
\( \Rightarrow \Delta OBE=\Delta ODE \) (c.c.c)
\( \Rightarrow \widehat{BOE}=\widehat{DOE}\) ( 2 góc tương ứng)
\( \Rightarrow \) OE là phân giác \(\widehat {xOy}\)
Bạn bổ sung đề đi bạn