Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

1/ vì xoy > xom
=> om nằm giữa ox , oy
vì thế ta có hệ thức : yom + mox = xoy
=> moy = xoy - mox = 80 - 60 = 20 độ
vì yom + mon = yon ( chứng minh om nằm giữa)
yom = mon = 20 độ ( chứng minh om cách điều oy , on)

a) Ta có: \(\widehat{mOx}=\widehat{mOn}+\widehat{nOx}=90^o\)
\(\Rightarrow\widehat{nOx}=90^o-\widehat{mOn}\) (1)
\(\widehat{nOy}=\widehat{mOn}+\widehat{mOy}=90^o\)
\(\Rightarrow\widehat{nOy}=90^o-\widehat{mOn}\) (2)
Từ (1), (2)
\(\Rightarrow\widehat{nOx}=\widehat{mOy}\) (đpcm)
b) Vì Ot là tia phân giác của \(\widehat{xOy}\) nên \(\widehat{xOt}=\widehat{tOy}\)
Mà \(\left\{{}\begin{matrix}\widehat{xOt}=\widehat{nOx}+\widehat{nOt}\\\widehat{tOy}=\widehat{mOy}+\widehat{mOt}\\\widehat{nOx}=\widehat{mOy}\end{matrix}\right.\Rightarrow\widehat{nOt}=\widehat{mOt}\) (3)
Lại có: Tia Ot nằm giữa 2 tia Om, On (4)
Từ (3), (4)
\(\Rightarrow\) Tia Ot cũng là tia phân giác của \(\widehat{mOn}\) (đpcm)
Dòng thứ tư bạn sửa lại hộ mình thành \(\widehat{mOy}=90^o-\widehat{mOn}\) nhé!

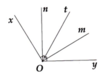
a) Theo tính chất cộng góc, ta có:
x O n ^ = x O y ^ − y O m ^ = 30 °
y O m ^ = x O y ^ − x O m ^ = 30 °
Vậy x O n ^ = y O m ^
b) Vì Ot là tia phân giác của góc xOy
nên: x O t ^ = y O t ^ = x O y ^ 2 = 60 °
Từ đó, ta có n O t ^ = x O t ^ − x O n ^ = 30 ° ; m O t ^ = y O t ^ − y O m ^ = 30 °
Mặt khác, m O n ^ = y O n ^ − y O m ^ = 60 °
Do đó, n O t ^ = m O t ^ = m O n ^ 2 (cùng bằng 30°).
Vậy Ot là tia phân giác của góc mOn.

a/ta có góc xoy+ góc oaz=30+150=180(ở vị trí trong cùng phía)
do đó AZ//OY ---> ZZ'/OY
b/ta có om là p/g của góc xoy --> góc AOm =75 độ
và on là p/g của góc oaz'--->góc oan=(180-30):2=75
mà hai góc trên ở vị trí so le trong
vậy AN//OM

Bài làm
~ Tự vẽ hình nha ~
a) Trên nửa mặt phẳng có bờ chứa tia Ox có:
\(\widehat{xOz}< \widehat{xOy}\left(50^0< 100^0\right)\)
=> Oz nằm giữa hai tia Ox và Oy.
b) Vì Oz nằm giữa hai tia Ox và Oy.
=> \(\widehat{xOz}+\widehat{yOz}=\widehat{xOy}\)
hay \(50^0+\widehat{yOz}=100^0\)
=> \(\widehat{yOz}=100^0-50^0\)
=> \(\widehat{yOz}=50^0\)
c) Ta có: \(\widehat{xOz}=50^0\)( theo đề bài )
Và \(\widehat{yOz}=50^0\)
=> \(\widehat{xOz}=\widehat{yOz=}50^0\)
=> Oz là tia phân giác của góc xOy
d) Trên nửa mặt phẳng có bờ chứa tia Ox có:
\(\widehat{xOz}< \widehat{xOm}\left(50^0< 70^0\right)\)
=> Oz nằm giữa hai tia Om và Ox.
Ta có: \(\widehat{xOz}+\widehat{mOz}=\widehat{xOm}\)
hay \(50^0+\widehat{mOz}=70^0\)
=> \(\widehat{mOz}=70^0-50^0=20^0\)
Vậy \(\widehat{mOz}=20^0\)