Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Kẻ MH; MK lần lượt vuông góc với Ox; Oy. Đặt MH = b; MK = a; HA = m; KB = n
+) Tam giác BKM đồng dạng với tam giác MHA (g- g) => BK / KM = MH / HA => n/a = b/ m => ab = m.n
a) S(AOB) = OA.OB/ 2
Ta có: OA = a + m ; OB = b + n
=> OA. OB = (a + m).(b + n) = ab + an + bm + mn = (ab + mn) + (an + bm)
= 2ab + (an + bm) \(\ge\) 2ab + \(2\sqrt{an.bm}\) = 2ab + \(2\sqrt{\left(ab\right)^2}\) = 4ab = hằng số ( M cố định nên a.b = MK.MH không đổi)
Dấu "=" xảy ra <=> an = bm => (an)2 = an.bm = (ab).(mn) = (mn)2 => a = m => H là trung điểm của OA
Vậy S(AOB) nhỏ nhất bằng 4ab khi H là trung điểm của OA
=> Vị trí đường thẳng d: d đi qua M và A, trong đó: A thuộc Ox sao cho H là trung điểm của OA
b) OA + OB = a + m + b + n = (a+ b) + (m + n) \(\ge\) a+ b + \(2\sqrt{mn}\) = a+ b + \(2\sqrt{ab}\) = \(\left(\sqrt{a}+\sqrt{b}\right)^2\) (vì m.n = ab)
Dấu "=" xảy ra <=> m = n => ab = n2
vậy OA + OB nhỏ nhất bằng \(\left(\sqrt{a}+\sqrt{b}\right)^2\) khi n2 = ab
+) Xác định vị trí của d sao cho n2 = ab = KB2
Cách dựng:
- Dựng đường tròn đường kính OK
- Trên đoạn OK , dựng KD = a. Qua D kẻ đường vuông góc với OK cắt đường tròn đường kính OK tại P
- Dựng đường tròn tâm K , bán kính KP cắt Oy tại B
- Đường thẳng đi qua B và M chính là đường thẳng d cần xác định
Chứng minh: Áp dụng hệ thức lượng trong tam giác vuông OPK có: KP2 = KD. KO = a.b
Mà KP = KB = n => n2 = ab
Vậy....


Đặt AC = x; BD = y (x, y > 0)
Ta có \(\Delta ACM\sim\Delta BMD\left(g-g\right)\Rightarrow\frac{AC}{MB}=\frac{AM}{BD}\)
\(\Rightarrow AC.BD=AM.MB=const\Rightarrow xy=c=const\)
\(S_{MCD}=S_{ACDB}-S_{ACM}-S_{MBD}=\frac{\left(x+y\right)\left(AM+MB\right)}{2}-\frac{x.AM}{2}-\frac{y.MB}{2}\)
\(=\frac{x.MB+y.AM}{2}\ge\sqrt{xy.MB.AM}=\sqrt{c^2}=c\)
Dấu bằng xảy ra khi x.MB = y.AM, lại có \(xy=MB.AM\Rightarrow\hept{\begin{cases}x=AM\\y=MB\end{cases}}\)
Vậy giá trị nhỏ nhất của \(S_{CMD}=c\left(đvdt\right)\) xảy ra khi AC = AM; BD = BM.

Em tham khảo tại link dưới đây nhé.
Câu hỏi của Linhllinh - Toán lớp 9 - Học toán với OnlineMath

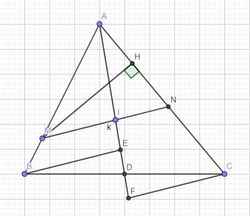
Từ M kẻ \(MH\perp AC\Rightarrow MH=AM.sinA\)
\(S_{AMN}=\dfrac{1}{2}MH.AB=\dfrac{1}{2}AM.AN.sinA\)
Mà góc A cố định \(\Rightarrow S_{min}\) khi \(AM.AN\) đạt min
Qua B, C lần lượt kẻ các đường thẳng song song d, cắt AD tại E và F
\(\Delta BDE=\Delta CDF\left(g.c.g\right)\Rightarrow DE=DF\)
Talet: \(\dfrac{AB}{AM}=\dfrac{AE}{AI}\) ; \(\dfrac{AC}{AN}=\dfrac{AF}{AI}\)
\(\Rightarrow\dfrac{AB}{AM}+\dfrac{AC}{AN}=\dfrac{AE+AF}{AI}=\dfrac{\left(AD-DE\right)+\left(AD+DF\right)}{AI}=\dfrac{2AD}{AI}\)
Do A; I; D cố định \(\Rightarrow\dfrac{2AD}{AI}\) cố định
\(\dfrac{2AD}{AI}=\dfrac{AB}{AM}+\dfrac{AC}{AN}\ge2\sqrt{\dfrac{AB.AC}{AM.AN}}\Rightarrow AM.AN\ge\dfrac{AB.AC.AI^2}{AD^2}\)
Đẳng thức xảy ra khi và chỉ khi \(\dfrac{AB}{AM}=\dfrac{AC}{AN}\Rightarrow d||BC\) theo Talet đảo