Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
qua O x lay D sao cho D diểm doi sung cua a qua O x lay E sao cho E ldiểm em doi sung cua a qua O y doan DE cat O x dâuau thdiểmem B ở do, DE cat O y dâuau thi C ở dó
de dang Cdượcoc tam Giác ABC có chu vi nhnhấtat
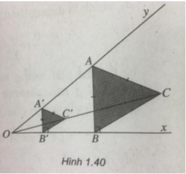
Giả sử điểm A đã dựng được . Gọi B là hình chiếu vuông góc của A trên Ox, khi đó AB = AC. Lấy điểm A' bất kì trên Oy, gọi B' là hình chiếu vuông góc của A' trên Ox, đường thẳng qua A' song song với AC cắt đường thẳng OC tại C'. Khi đó có thể coi tam giác ABC là ảnh của tam giác A'B'C' qua phép vị tự tâm O tỉ số A C A ' C ' nên A'C' = A'B'.
Từ đó suy ra cách dựng:
- Lấy điểm A bất kì trên Oy, dựng B' là hình chiếu vuông góc của A lên Ox
- Lấy C' là một giao điểm của đường tròn tâm A' bán kính A'B' với đường thẳng OC.
- Đường thẳng qua C song song với A'C' cắt Oy tại A.
Dễ thấy A là điểm phải dựng.
Bài toán có hai nghiệm hình.
Đáp án A
Lấy A’, A” lần lượt là điểm đối xứng với A qua Ox và Oy
Tacó:
AB + AC + BC = BA’ + CA” + BC ≥ A’A” Chu vi tam giác ABC:
Dấu bằng xảy ra khi A’, A” , B , C thẳng hàng
Đáp án là C
Số tứ giác có 4 đỉnh là 4 điểm trong 13 điểm đã cho là C 8 2 . C 5 2 = 280
Mỗi tứ giác đó có hai đường chéo cắt nhau tại 1 điểm thuộc góc phần tư thứ nhất của hệ tọa độ Oxy
Vậy số giao điểm là 280.
Chọn B
· Bổ đề: Trong mặt phẳng cho hai tia Ox và Oy vuông góc với nhau tại gốc O. Trên tia Ox lấy 10 điểm A 1 , A 2 , . . . , A 10 và trên tia Oy lấy 10 điểm B 1 , B 2 , . . . . , B 10 thỏa mãn O A 1 = A 1 A 2 = . . . = A 9 A 10 = O B 1 = B 1 B 2 = . . . . = B 9 B 10 = 1 (đvd).
Tìm số tam giác có 2 đỉnh nằm trong 10 điểm 
1 đỉnh nằm trong 10 điểm
B
1
,
B
2
,
.
.
.
.
,
B
10
sao cho tam giác chọn được có đường tròn ngoại tiếp, tiếp xúc với một trong hai trục Ox hoặc Oy?
Giải: Gọi 
là 3 đỉnh của tam giác thỏa yêu cầu bài toán với 
Ta có 
Do đường tròn luôn cắt Ox tại 
phân biệt nên đường tròn chỉ có thể tiếp xúc với Oy tại
B
p
ta có phương tích
Do 
nên dễ thấy 
hay nói cách khác bộ ba (m,n,p) 
Vậy có 4 tam giác thỏa mãn yêu cầu bổ đề.
· Bài toán: Không gian mẫu 
Gọi A là biến cố chọn được tam giác có đường tròn ngoại tiếp tiếp xúc với một trong hai trục Ox hoặc Oy. Theo bổ đề ta chọn được 4 tam giác có 2 đỉnh thuộc tia Ox, 1 đỉnh thuộc tia Oy; tương tự có 4 tam giác có 1 đỉnh thuộc tia Oy, đỉnh thuộc tia . Suy ra, n(A) = 8
Xác suất biến cố A là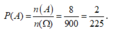 
Lấy A’’ đối xứng với A qua d.
Chu vi tam giác ABC = AB + AC + BC = AB + CA’’+ CB
Vì độ dài AB không đổi nên để chu vi tam giác ABC nhỏ nhất khi và chỉ khi CA” + CB nhỏ nhất.
Lại có; C A " + C B ≥ A " B
Do đó, để chu vi tam giác ABC nhỏ nhất khi và chỉ khi CA” + CB = A”B. Khi đó: B, C, A’’ thẳng hàng.
Đáp án C
- Tìm A’ đối xứng với A qua Oy , B’ đối xứng với A qua Ox
- Nối A’B’ cắt Ox tại B , cắt Oy tại C . Đó chính là hai điểm cần tìm
- Chứng minh B,C là hai điểm duy nhất cần tìm .
Thật vậy : Do A’ đối xứng với A qua Oy , cho nên CA=CA’ (1) . Mặt khác : B’ đối xứng với A qua Ox cho nên ta có BA=BB’ (2) .
Gọi P là chu vi tam giác ABC - do từ (1) và (2) - thì P=CA+CB+BA =CA’+CB+BB’=A’B’