Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Phần b thêm là chứng minh OE là tia phân giác của gíc Xoy nhé mình nhầm
"Non sông Việt Nam có trở nên vẻ vang hay không, dân tộc Việt Nam có được vẻ vang sánh vai các cường quốc năm châu hay không chính là nhờ một phần lớn ở công học tập của các cháu".
Sinh thời, Chủ tịch Hồ Chí Minh luôn dành nhiều tình cảm và kỳ vọng lớn lao vào thế hệ trẻ của nước nhà. Trong thư gửi cho học sinh nhân ngày khai trường mùa Thu năm 1945, Người đã căn dặn các thế hệ học sinh như vậy.
Năm 1956, Đại hội Thành lập Hội Liên hiệp Thanh niên Việt Nam diễn ra tại thủ đô Hà Nội đã vinh dự được đón Chủ tịch Hồ Chí Minh. Tại Đại hội, Người đã căn dặn toàn thể thanh niên nước nhà: Đoàn kết phấn đấu, vui vẻ, mạnh dạn, tiến bộ là gì? Là để mà giúp sức vào xây dựng một nước Việt Nam Hòa bình, thống nhất, độc lập, dân chủ và giàu mạnh”.

a) Xét ▲OAD và ▲OBC có :
OA = OB ( gt )
góc COD chung
OC = OD ( gt )
=> ▲OAD = ▲OBC ( c-g-c )
=> đpcm
b) Gọi giao điểm của BC và AD là M
Vì ▲OAD = ▲OBC ( c/m trên )
=> góc OCB = góc ODA ( 2 góc tương ứng )
Xét ▲ACM có góc MAC + góc ACM + góc CMA = 1800
Xét ▲BMD có góc BMD + góc MDB + góc DBM = 1800
Mà góc OCB = góc ODA ( c/m trên ) và góc CMA = góc BMD ( đối đỉnh )
=> góc CAM = góc MBD ( đpcm )

a) Xét \(\Delta AOD\)và \(\Delta\)BOC có:
OA=OB (gt)
\(\widehat{O}\)chung
OD=OC (gt)
=> \(\Delta AOD=\Delta BOC\left(cgc\right)\)
=> AD=BC (2 cạnh tương ứng) (đpcm)
b) Ta có: \(\hept{\begin{cases}OC=OD\\OA=OB\end{cases}\Rightarrow OC-OA=OD-OB\Leftrightarrow AC=BD}\)
Xét tam giác EBD và tam giác EAC có:
AC chung
\(\widehat{DBE}=\widehat{CAE}\)
\(\widehat{BDE}=\widehat{ECA}\)
\(\Rightarrow\Delta EBD=\Delta EAC\left(gcg\right)\)
=> DE=EC (2 cạnh tương ứng)
Xét tam giác OED và tam giác OEC có:
OD=OC (gt)
OE chung
DE=EC (cmt)
=> \(\Delta OED=\Delta OEC\left(ccc\right)\)
=> \(\widehat{DOE}=\widehat{COE}\)(2 góc tương ứng)
=> OE là phân giác \(\widehat{xOy}\)(đpcm)
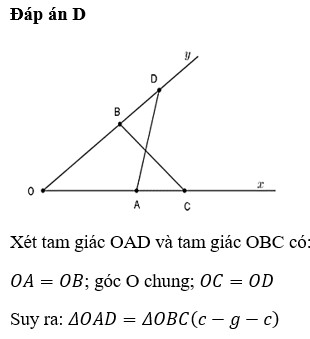
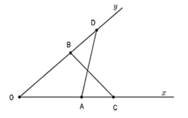




Xét ∆OAD và ∆OBC ta có:
OC = OD (gt)
∠COB = ∠AOD
OA = OB (gt)
⇒ ∆OAD = ∆OBC (c.g.c)
Do đó: AD = BC
Vì AC = OC - OA ; BD = OD - OB
Nên AC = BD (∆OAD = ∆OBC)
Xét ∆ACD và ∆DBC ta có:
AD = BC
AC = BD
CD là cạnh chung
⇒ ∆ACD = ∆DBC (c.c.c)
Do đó: ∠CAD = ∠CBD