
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



a: \(\left\{{}\begin{matrix}3x+6y=4\\x+4y=2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=\dfrac{1}{3}\\x=\dfrac{2}{3}\end{matrix}\right.\)

c: Thay y=-x vào (P), ta được:
-x^2=-x
=>x^2=x
=>x(x-1)=0
=>x=0 hoặc x=1
Khi x=0 thì y=0
Khi x=1 thì y=-1
Vậy: Điểm cần tìm là M(1;-1) hoặc O(0;0)

a: Xét (O) có
MA là tiếp tuyến
MB là tiếp tuyến
Do đó: MA=MB
hay M nằm trên đường trung trực của AB(1)
Ta có: OA=OB
nên O nằm trên đường trung trực của AB(2)
Từ (1) và (2) suy ra OM⊥AB

20.
Đặt \(\left(x;y;z\right)=\left(a^3;b^3;c^3\right)\Rightarrow abc=1\)
\(a^3+b^3=\left(a+b\right)\left(a^2+b^2-ab\right)\ge\left(a+b\right)\left(2ab-ab\right)=ab\left(a+b\right)\)
\(\Rightarrow P=\sum\dfrac{1}{a^3+b^3+1}\le\sum\dfrac{1}{ab\left(a+b\right)+1}=\sum\dfrac{abc}{ab\left(a+b\right)+abc}=\sum\dfrac{c}{a+b+c}=1\)
21.
Đề bài sai, biểu thức này ko tồn tại min hay max (nó chỉ tồn tại khi x;y;z là số thực không âm. Khi đó min P xảy ra tại \(\left(x;y;z\right)=\left(\dfrac{1}{2};\dfrac{1}{2};0\right)\) và hoán vị)
22.
Đề bài sai, biểu thức không tồn tại min. Nó chỉ tồn tại khi có thêm điều kiện x;y;z là độ dài 3 cạnh của 1 tam giác (em cứ thay giá trị \(x=2;y=1.9999;z=8.0001\) vào tính giá trị P sẽ hiểu tại sao đề sai)

a) \(BC^2=AB^2+AC^2\Rightarrow BC=\sqrt{AB^2+AC^2}=\sqrt{3^2+4^2}=5\left(cm\right)\)
\(\left\{{}\begin{matrix}sinB=\dfrac{AC}{BC}=\dfrac{4}{5}\Rightarrow\widehat{B}\approx53^0\\sinC=\dfrac{AB}{BC}=\dfrac{3}{5}\Rightarrow\widehat{C}=37^0\end{matrix}\right.\)
c) Ta có: \(\left\{{}\begin{matrix}AB=BD\\AC=DC\end{matrix}\right.\)(t/c 2 tiếp tuyến cắt nhau)
=> BC là đường trung trực AD
\(\Rightarrow AD\perp BC\)
Áp dụng HTL trong tam giác BDC vuông tại D:
\(FB.FC=FD^2\Rightarrow4FB.FC=4FD^2=\left(2FD\right)^2=AD^2\)


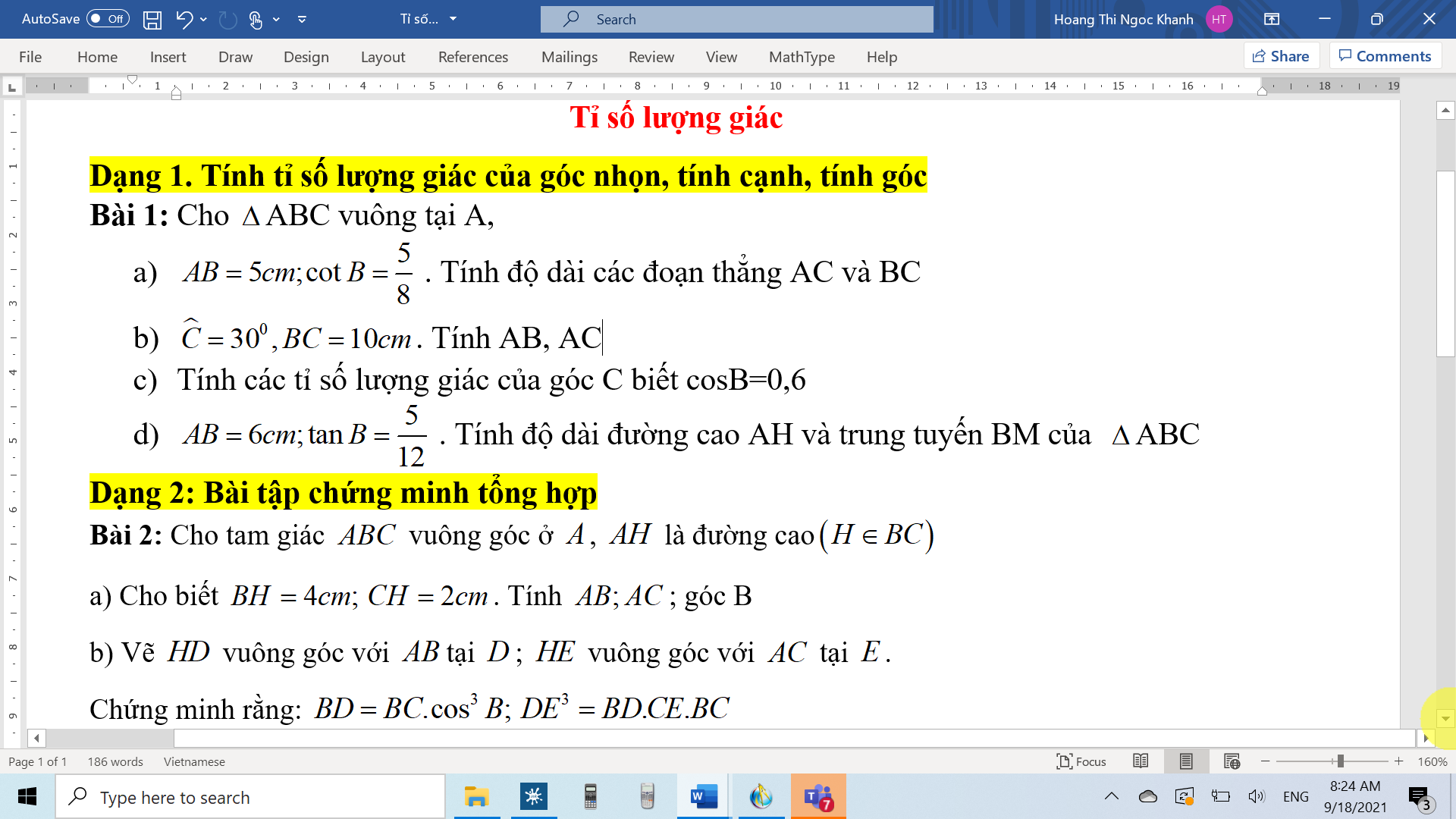






Bài 2:
b. \(\sqrt{\left(3x+1\right)^2}=25\)
<=> \(|3x+1|=25\)
<=> \(\left[{}\begin{matrix}3x+1=-25\\3x+1=25\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{-26}{3}\\x=8\end{matrix}\right.\)
Bài 3:
Ta có: \(\dfrac{5}{\sqrt{7}+\sqrt{2}}+\dfrac{2}{3+\sqrt{7}}+\dfrac{2-\sqrt{2}}{\sqrt{2}-1}\)
\(=\sqrt{7}-\sqrt{2}+3-\sqrt{7}+\sqrt{2}\)
=3