K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên

30 tháng 5 2023
a: góc ABO+góc ACO=180 độ
=>ABOC nội tiếp
b: Xét ΔOBA vuông tại B có sin BAO=OB/OA=1/2
nên góc BAO=30 độ
Xét ΔOBI có OB=OI và góc BOI=60 độ
nên ΔOBI đều
=>OI=OB=1/2OA
=>AI*AO=2R^2
Xét ΔBDE vuông tại D có DC vuông góc BE
nên ΔBDE vuông tại D
=>BC*BE=BD^2=4R^2
=>BC*BE+AI*AO=6R^2

CM
10 tháng 3 2019
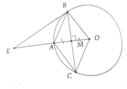
a, OA vuông góc với BC tại M
=> M là trung điểm của BC
=> OCAB là hình thoi
b, Tính được BE = R 3

24 tháng 6 2017
a) tứ giác ABOC là hình vuông
vì BAC = 90 (giả thiết)
ABO = 90 (AB là tiếp tuyến)
ACO = 90 (AC là tiếp tuyến)
AB = AC (tính chất 2 tiếp tuyến cắt nhau)


a:
Xét (O) có
AB,AC là tiếp tuyến
Do đó: AB=AC; OA;AO lần lượt là phân giác của \(\widehat{BOC};\widehat{BAC}\)
Xét ΔOBA vuông tại B có \(cosBOA=\dfrac{OB}{OA}=\dfrac{1}{\sqrt{2}}\)
=>\(\widehat{BOA}=45^0\)
OA là phân giác của \(\widehat{BOC}\)
=>\(\widehat{BOC}=2\cdot\widehat{BOA}=90^0\)
Xét tứ giác OBAC có \(\widehat{OBA}=\widehat{BOC}=\widehat{OCA}=90^0\)
nên OBAC là hình chữ nhật
Hình chữ nhật OBAC có OB=OC
nên OBAC là hình vuông
b: Xét (O) có
DM,DB là tiếp tuyến
Do đó: OD là phân giác của góc BOM và DB=DM
Xét (O) có
EM,EC là tiếp tuyến
Do đó: EM=EC và OE là phân giác của góc MOC
\(\widehat{DOE}=\widehat{DOM}+\widehat{MOE}\)
\(=\dfrac{1}{2}\left(\widehat{BOM}+\widehat{MOC}\right)\)
\(=\dfrac{1}{2}\cdot\widehat{BOC}=\dfrac{1}{2}\cdot90^0=45^0\)
c: Gọi giao điểm của OA và BC là H
AB=AC
OB=OC
Do đó: OA là đường trung trực của BC
=>OA\(\perp\)BC tại H và H là trung điểm của BC
\(\widehat{KBA}+\widehat{KBO}=\widehat{OBA}=90^0\)
\(\widehat{CBK}+\widehat{BKO}=90^0\)(ΔBHK vuông tại H)
mà \(\widehat{OBK}=\widehat{OKB}\)(OK=OB)
nên \(\widehat{KBA}=\widehat{CBK}\)
=>BK là phân giác của góc ABC
Xét ΔABC có
BK,AK là các đường phân giác
Do đó: K là tâm đường tròn nội tiếp ΔABC