Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

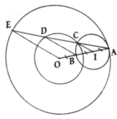
a, Gọi I là trung điểm của AB, ta có: OI = OA – IA
b, Ta chứng minh được IC//BD//OE
Mà OB = BI = IA => AC = CD = DE

a) Gọi d là tiếp tuyến tại A của đường tròn (O) => d vuông góc OA => d vuông góc AB
Vì AB là đường kính của đường tròn (AB) nên d cũng là tiếp tuyến của (AB)
Vậy (O) và (AB) tiếp xúc nhau tại A (đpcm).
b) Gọi I là trung điểm đoạn AB => I là tâm của (AB) => ^ICA = ^IAC = ^OEA => IC // OE
Ta thấy OB = BI = IA = OA/3 => \(\frac{AI}{AO}=\frac{1}{3}\). Áp dụng ĐL Thales vào \(\Delta\)AEO có
\(\frac{AC}{AE}=\frac{AI}{AO}=\frac{1}{3}\) => AC = 1/3.AE (1)
Gọi OC,OD cắt đường tròn (O) cho trước lần lượt tại F,G. Khi đó DC // GF
Hay GF // AE. Mà GF và AE là các dây của đường tròn (O) nên (GE = (AF => ^EOG = ^AOF
Xét \(\Delta\)ODE và \(\Delta\)OCA: OD = OC, ^EOD = ^AOC (cmt), OE = OA => \(\Delta\)ODE = \(\Delta\)OCA (c.g.c)
=> ED = AC. Kết hợp với (1) suy ra AC = DE = AE/3 => AC = CD = DE (đpcm).

Bài 2 nếu ai giải được thì làm ơn gửi cho mình cách giải nhé!!Mình cũng có bài này mà ko giải được

Cho đường tròn (O) và dây cung AB( AB không phải là đường kính) cố định. P là điểm di động trên đoạn AB.( P khác A,B và P khác trung điểm của AB). Đường tròn tâm C, D đi qua điểm P tiếp xúc với đường tròn (O) lần lượt tại A và B. Hai đường tròn (C) , (D). cắt nhau tại N( N khác P) . CMR:
a. ˆANP=ˆBNPANP^=BNP^ và 4 điểm O,D,C,N cùng thuộc 1 đường tròn.
b. Đường trung trực của ON luôn đi qua điểm cố định khi P di động