Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xét (O) có
ΔACB nội tiếp
AB là đường kính
=>ΔABC vuông tại C
=>AC vuông góc CB
=>CB vuông góc BD
=>B nằm trên đường tròn đường kính CD
Xét tứ giác ACBD có
AB căt CD tại trung điểm của mỗi đường
AB=CD
=>ACBD là hình chữ nhật
=>AC=BD
b:
Th1: AC<BC
mà OM,ON lần lượt là khoảng cách từ O đến AC,BC
nên OM>ON
TH2:
AC>BC
mà OM,ON lần lượt là khoảng cách từ O đến AC,BC
nên OM<ON
TH3:
AC=BC
mà OM,ON lần lượt là khoảng cách từ O đến AC,BC
nên OM=ON

a) Xét tam giác BEC
Ta có :
tam giác BEC nt (O)
BC đường kính
=> tam giác BEC vuông tại E
Xét tam giác BDC
Ta có :
tam giác BDC nt (o)
BC đường kính
=> tam giác BDC vuông tại D
Ta có:
góc BEC vuông tại E
góc BDC vuông tại D
Mà EC cắt DB tại H
=> H là trực tâm
=> AH vuông góc Với BC tại F
c) Xét tg BEHF
Ta có
góc BEH= 90 độ
góc BFH = 90 độ
=> góc BEC + góc BDC = 90 độ + 90 độ = 180 độ
=> tg BEHF nt(tổng 2 góc đối bằng 180 độ )
Ta có: B, E, D, F thuộc (O)
=> tg BEDF nt (O)
=> góc EBD = góc EFD ( 1 )
ta có: tg BEHF nt
=> góc EBH = góc EFH ( 2 )
từ (1) và (2)
=> góc EFD = góc EFH
=> AF // AF

Cô hướng dẫn nhé. :)
Tứ giác AIDE nội tiếp đường tròn đường kính AI.
b. Do câu a ta có AIDE là tứ giác nội tiếp nên gó IDE = góc IAE. Lại có góc IAE = góc CDB. Từ đó suy ra DB là tia phân giac góc CDE.
c. Ta thấy góc CDE = 2 góc CAB (Chứng minh b). Lại có góc COB = 2 góc CAB. Từ đó suy ra góc CDE = góc COB. Hay OEDC là tứ giác nội tiếp ( Góc ngoài ở đỉnh bằng góc đối diện )
Chúc em học tốt ^^

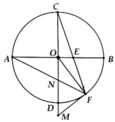
a, Học sinh tự chứng minh
b, Chứng minh: A F M ^ = C A F ^ ( = A C F ^ ) => MF//AC
c, Chứng minh: M F N ^ = M N F ^ => ∆MNF cân tại M => MN = MF
Mặt khác: OD = OF = R
Ta có MF là tiếp tuyến nên DOFM vuông => ĐPCM