Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

câu a
Gọi H là chân đường vuông góc hạ từ M xuống tia phân giác ^BAC. Tam giác ADE có AH vừa là phân giác vùa là đường cao nên cân tại A.
Qua B vẽ BF//CE (F thuộc DE) => tam giác BDF cân tại B => BD = BF (1)
Mặt khác xét 2 tam giác BMF và CME có : BM = CM; ^BMF = ^CME ( đối đỉnh); ^MBF = ^MCE ( so le trong) => tam giác BMF = tg CME => BF = CE (2)
Từ (1) và (2) => đpcm
mấy câu còn lại bó tay

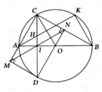
a, Tứ giác BIHK nội tiếp (tổng hai góc đối bằng 180 0 )
b, Chứng minh AH.AK = AI.AB = 1 2 R.2R = R 2 => ĐPCM
c, MCND là hình chữ nhật => MN, AB, CD đồng quy tại I là trung điểm của CD
d, Tam giác OCA đều => A B C ^ = 30 0 ; M C D ^ = 60 0
Tính được CD = 2CI = 2 . 25 2 = 25cm; CM = 25 2 cm, MD = 25 3 2 cm, Sxq = 2.π.CM.MD = 625 3 2 πcm 2