Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

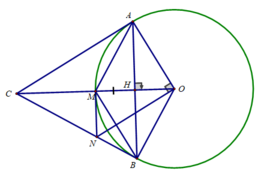
b) Chứng minh tứ giác OAMB là hình thoi.
Do H là trung điểm của AB (cmt)
H là trung điểm của OM
nên tứ giác OAMB là hình bình hành mà OM vuông góc AB.
Vậy tứ giác OAMB là hình thoi.

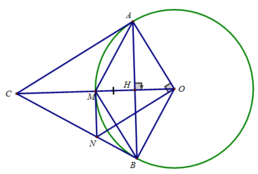
d) Ta có: CA ⊥ OA (CA là tiếp tuyến của (O)
và ON ⊥ OA (gt)
⇒ CA // ON ⇒ ∠(CON) = ∠(ACO) (sole trong)
Mà ∠(ACO) = ∠(BCO) (ΔOAC = ΔOBC)
⇒ ∠(CON) = ∠(BCO) ⇒ ΔNCO cân tại N
Xét tam giác CAO vuông tại A có ∠(AOC) = 60o( ΔAMO đều) nên:
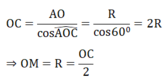
⇒ M là trung điểm của OC
ΔNCO cân tại N có NM là trung tuyến ⇒ NM cũng là đường cao
Hay NM là tiếp tuyến của (O)

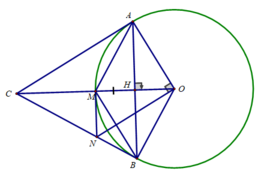
c) Xét ΔOAC và ΔOBC có:
OA = OB = R
∠(AOC) = ∠(BOC) (tính chất đường chéo hình thoi)
OC là cạnh chung
⇒ ΔOAC = ΔOBC (c.g.c)
⇒ AC = BC

a) zì H là trung điểm của AB nên \(OH\perp AB\)hay \(\widehat{OHM}=90^0\)
theo tính chất của tiếp tuyến ta lại có \(OD\perp DM\left(hay\right)\widehat{ODM}=90^0\)
=> M,D,O,H cùng nằm trên 1đường tròn
b) Theo tính chất tiếp tuyến ta có
MC=MD=> tam giác MDC cân tại M
=> MI là 1 đương phân giác của CMD , MẶt khác I là điểm chính giữa cung nhỏ CD nên :
\(\widehat{DCI}=\frac{1}{2}sđ\widebat{DI}=\frac{1}{2}sđ\widebat{CI}=\widehat{MCI}\)
=> CI là phân giác của góc MCD .
zậy I là tâm đường tròn nội tiếp tam giác MCD

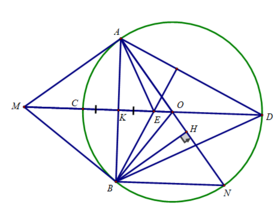
d) Ta có:
K là trung điểm của CE (E đối xứng với C qua AB)
K là trung điểm của AB
AB ⊥ CE (MO ⊥ AB)
⇒ Tứ giác AEBC là hình thoi
⇒ BE // AC
Mà AC ⊥ AD (A thuộc đường tròn đường kính CD)
Nên BE ⊥ AD và DK ⊥ AB
Vậy E là trực tâm của tam giác ADB
a) Chứng minh H là trung điểm của AB
Ta có OM vuông góc AB tại H (gt)
Vậy H là trung điểm của AB (đường kính vuông góc với một dây cung)
Chứng minh tam giác OAM đều:
Ta có: AM = AO (A là trung trực của OM)
và OA = OM = R
Suy ra AM = AO = OM
Vậy ΔOAM đều.