Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

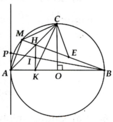
a, Chứng minh được H C B ^ = H K B ^ = 90 0
b, A C K ^ = H B K ^ (CBKH nội tiếp)
Lại có: A C M ^ = H B K ^ = 1 2 s đ A M ⏜
=> A C M ^ = A C K ^
c, Chứng minh được:
DMCA = DECB (c.g.c) => MC = CE
Ta có: C M B ^ = C A B ^ = 1 2 s đ C B ⏜ = 45 0
=> DMCE vuông cân tại C
d, Gọi P B ∩ H K = I
Chứng minh được DHKB đồng dạng với DAMB (g.g)
=> H K K B = M A M B = A P R => H K = A P . B K R
Mặt khác: ∆BIK:∆BPA(g.g) => (ĐPCM)

1: góc BCA=1/2*180=90 độ
góc HKB+góc HCB=180 độ
=>HCBK nội tiếp
2: góc ACM=1/2*sđ cung AM
góc ACK=góc HCK=góc MBA=1/2*sđ cung AM
=>góc ACM=góc ACK

a: Xét (O) có
ΔACB nội tiếp
AB là đường kính
Do đó: ΔACB vuông tại C
Xét tứ giác HCBK có
\(\widehat{HCB}+\widehat{HKB}=180^0\)
Do đó: HCBK là tứ giác nội tiếp
b: Vì HCBK là tứ giác nội tiếp
nên \(\widehat{ACK}=\widehat{HBK}\)
mà \(\widehat{ACM}=\widehat{HBK}\left(=\dfrac{sđ\stackrel\frown{AM}}{2}\right)\)
nên \(\widehat{ACM}=\widehat{ACK}\)

1: góc ACB=1/2*180=90 độ
góc HKB+góc HCB=180 độ
=>CBKH nội tiếp
2: góc MCA=1/2*sđ cung MA
góc ACK=góc MBA=1/2*sđ cung MA
=>góc MCA=góc KCA
=>CA là phân giác của góc MCK

Câu a dễ nha: tứ giác BCDO có DOB+DCB=90+90=180(mà 2 góc ở vị trí đối nhau )
nên BCDO nội tiếp
câu b) tam giác ADO và tam giác ABC có:
góc BAC chung
AOD=ACB=90
câu c: CB là dây cung mà OE là đường thẳng đi qua bán kính nên OE vuông góc với BC
nên OE// DC hay AD//OE mà DE//AO nên OEDA là hình bình hành
câu d thì mk chưa nghĩ ra hihi thông cảm nha
ở câu c nếu chỉ có BC là dây và OE là đường thẳng đi qua bán kính thì BC chưa thể vuông góc với OE được bạn nhé mà cần phải OE đi qua trung điểm của BC nữa
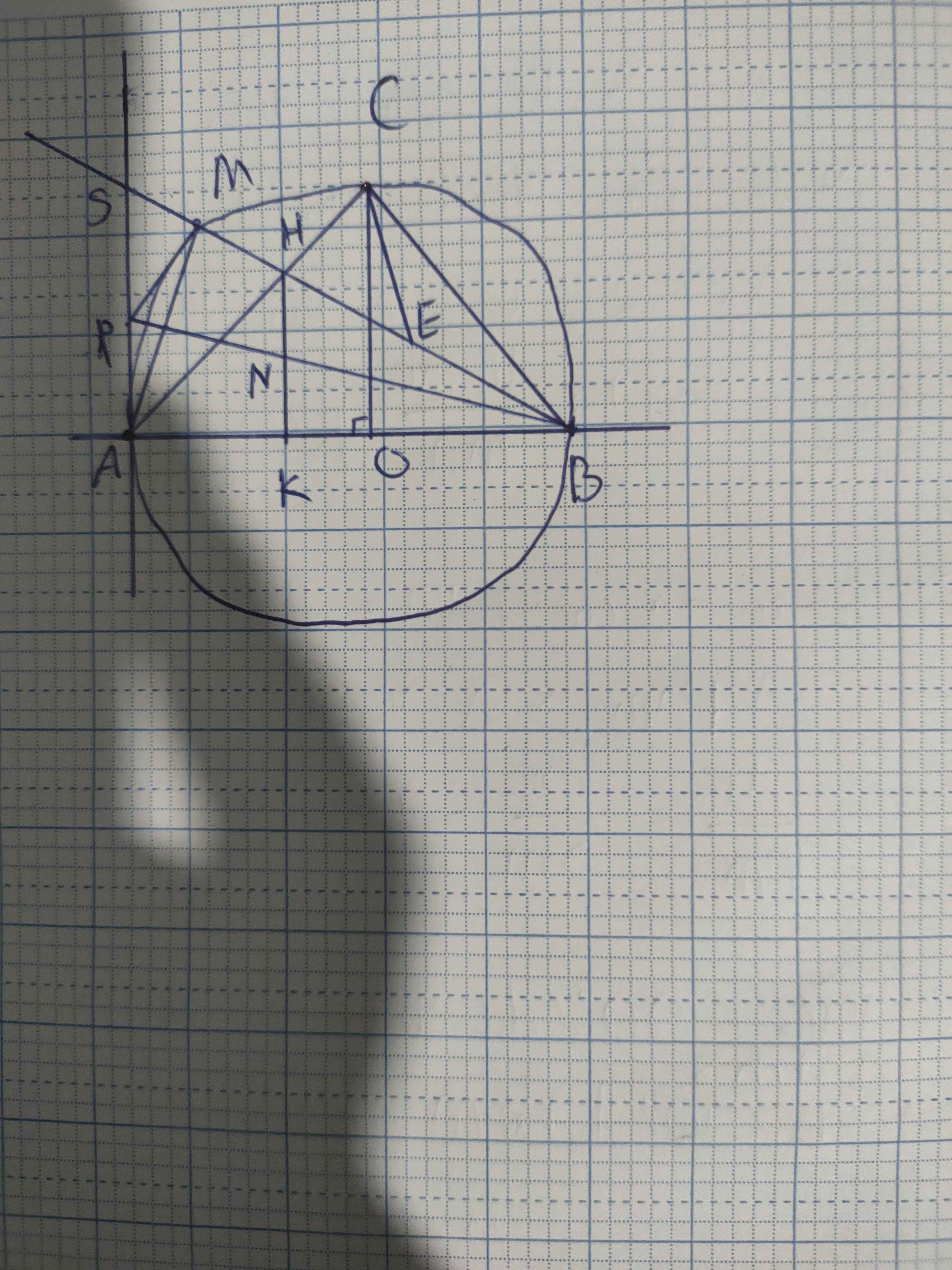


O A B C M K H E d P F I
1) Dễ thấy \(\widehat{HCB}=\widehat{ACB}=90^o\)
tứ giác CBKH có \(\widehat{HKB}=\widehat{HCB}=90^o\)nên là tứ giác nội tiếp
\(\Rightarrow\widehat{HCK}=\widehat{HBK}\)( 1 )
Mà \(\widehat{ACM}=\widehat{ABM}=\frac{1}{2}sđ\widebat{AM}\)( 2 )
Từ ( 1 ) và ( 2 ) suy ra \(\widehat{ACM}=\widehat{ACK}\)
2) Xét \(\Delta AMC\)và \(\Delta BEC\)có :
AM = BE ; AC = BC ; \(\widehat{MAC}=\widehat{CBE}=\frac{1}{2}sđ\widebat{MC}\)
\(\Rightarrow\Delta AMC=\Delta BEC\)( c.g.c )
\(\Rightarrow MC=EC\)
Ta có : \(\widehat{CMB}=\frac{1}{2}sđ\widebat{BC}=45^o\)
Suy ra \(\Delta ECM\)vuông cân tại C
3) Ta có : \(\frac{AP.MB}{AM}=R=OB\Rightarrow\frac{AP}{MA}=\frac{OB}{MB}\)
Xét \(\Delta APM\)và \(\Delta OBM\), ta có :
\(\frac{AP}{MA}=\frac{OB}{MB}\); \(\widehat{PAM}=\widehat{MBO}=\frac{1}{2}sđ\widebat{AM}\)
\(\Rightarrow\Delta APM\approx\Delta BOM\left(c.g.c\right)\)
\(\Rightarrow\Delta APM\)cân tại P ( vì \(\Delta BOM\)cân tại O )
\(\Rightarrow PA=PM\)
Gọi giao điểm của BM và ( d ) là F ; giao điểm của BP với HK là I
Xét tam giác vuông AMF có PA = PM nên PA = PM = PF
Theo định lí Ta-let, ta có :
\(\frac{HI}{FP}=\frac{BI}{BP}=\frac{KI}{AP}\Rightarrow HI=KI\)
vì vậy PB đi qua trung điểm của HK