Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Xét tứ giác OAMC có
\(\widehat{OAM}\) và \(\widehat{OCM}\) là hai góc đối
\(\widehat{OAM}+\widehat{OCM}=180^0\left(90^0+90^0=180^0\right)\)
Do đó: OAMC là tứ giác nội tiếp(Dấu hiệu nhận biết tứ giác nội tiếp)

a: góc OAM+góc OCM=180 độ
=>OAMC nội tiếp
b: CE//BD
=>góc AKM=góc AEC=góc ACM
=>AKCM nội tiếp
=>A,K,C,M cùng nằm trên 1 đường tròn
=>góc OKM=90 độ
=>K là trung điểm của BD

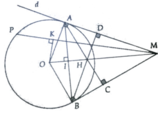
a, HS tự làm
b, Chú ý O K M ^ = 90 0 và kết hợp ý a) => A,M,B,O,K ∈ đường tròn đường kính OM
c, Sử dụng hệ thức lượng trong tam giác vuông OAM ( hoặc có thể chứng minh tam giác đồng dạng)
d, Chứng minh OAHB là hình bình hành và chú ý A,B thuộc (O;R) suy ra OAHB là hình thoi
e, Chứng minh OH ⊥ AB, OMAB => O,H,M thẳng hàng