Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

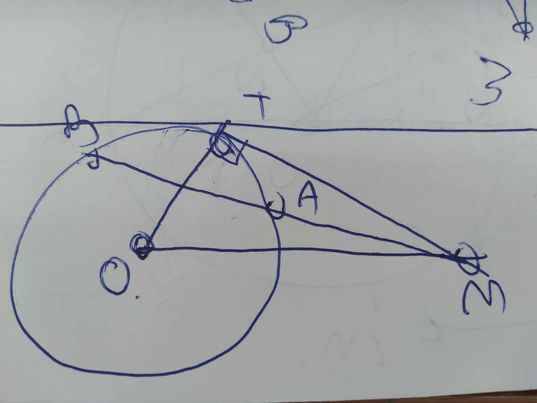
Xét đường tròn (O;R) có \(\widehat{MTA}\)là góc tạo bởi tiếp tuyến MT (tiếp điểm là T) và dây cung TA \(\Rightarrow\widehat{MTA}=\frac{1}{2}sđ\widebat{TA}\)
Mà \(\widehat{MBT}\)là góc nội tiếp chắn cung TA \(\Rightarrow\widehat{MBT}=\frac{1}{2}sđ\widebat{TA}\)
\(\Rightarrow\widehat{MTA}=\widehat{MBT}\left(=\frac{1}{2}sđ\widebat{TA}\right)\)
Xét \(\Delta MTA\)và \(\Delta MBT\), ta có: \(\widehat{BMT}\)chung; \(\widehat{MTA}=\widehat{MBT}\left(cmt\right)\)
\(\Rightarrow\Delta MTA~\Delta MBT\left(g.g\right)\)\(\Rightarrow\frac{MT}{MB}=\frac{MA}{MT}\Rightarrow MT^2=MA.MB\)(1)
Hoàn toàn tương tự, ta có \(MT^2=MC.MD\)(2)
Vì MT là tiếp tuyến tại T của (O) \(\Rightarrow MT\perp OT\)tại T \(\Rightarrow\Delta OMT\)vuông tại T
\(\Rightarrow OM^2=MT^2+OT^2\)\(\Rightarrow MT^2=OM^2-OT^2\)
Đồng thời MT là tiếp tuyến tại T của (O;R) \(\Rightarrow OT=R\)
Như vậy ta có \(MT^2=OM^2-R^2\)(3)
Từ (1), (2) và (3) ta có đpcm.

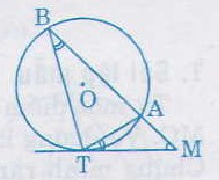
Xét ΔOTM vuông tại T có \(OM^2=OT^2+TM^2\)
=>\(TM^2=OM^2-OT^2\)
=>\(MT^2=d^2-R^2\left(1\right)\)
Xét (O) có
\(\widehat{MTA}\) là góc tạo bởi tiếp tuyến TM và dây cung TA
\(\widehat{TBA}\) là góc nội tiếp chắn cung TA
Do đó: \(\widehat{MTA}=\widehat{TBA}\)
=>\(\widehat{MTA}=\widehat{MBT}\)
Xét ΔMTA và ΔMBT có
\(\widehat{MTA}=\widehat{MBT}\)
\(\widehat{TMA}\) chung
Do đó: ΔMTA đồng dạng với ΔMBT
=>\(\dfrac{MT}{MB}=\dfrac{MA}{MT}\)
=>\(MT^2=MA\cdot MB\left(2\right)\)
Từ (1) và (2) suy ra \(MA\cdot MB=MT^2=d^2-R^2\)

Xét ΔOTM vuông tại T có \(OM^2=OT^2+TM^2\)
=>\(TM^2=OM^2-OT^2\)
=>\(MT^2=d^2-R^2\left(1\right)\)
Xét (O) có
\(\widehat{MTA}\) là góc tạo bởi tiếp tuyến TM và dây cung TA
\(\widehat{TBA}\) là góc nội tiếp chắn cung TA
Do đó: \(\widehat{MTA}=\widehat{TBA}\)
=>\(\widehat{MTA}=\widehat{MBT}\)
Xét ΔMTA và ΔMBT có
\(\widehat{MTA}=\widehat{MBT}\)
\(\widehat{TMA}\) chung
Do đó: ΔMTA đồng dạng với ΔMBT
=>\(\dfrac{MT}{MB}=\dfrac{MA}{MT}\)
=>\(MT^2=MA\cdot MB\left(2\right)\)
Từ (1) và (2) suy ra \(MA\cdot MB=MT^2=d^2-R^2\)

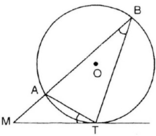
Xét hai tam giác BMT và TMA, chúng có:
chung
=
(cùng chắn cung nhỏ
![]() )
)
nên ∆BMT ~ ∆TMA, suy ra =
hay MT2 = MA. MB

bài này dễ mà bạn
có MTA=1/2 sd AT
ABT=1/2 sd AT
\(\Rightarrow\)MTA=MTB
xét tam giác MTA và MBT
M chung
MTA=MTB
tam giác MTA dong dang MBT
\(\Rightarrow\)MT/AB=MA/MT\(\Rightarrow\)MT2=MA.MT


( góc tạo bởi tia tiếp tuyến và dây cung, góc nội tiếp cùng chắn cung AT)

Kiến thức áp dụng
Trong một đường tròn, góc tạo bởi tia tiếp tuyến và dây cung và góc nội tiếp cùng chắn một cung thì bằng nhau.

góc mta và góc mbt cùng bằng gì vậy bạn