Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Kẻ I là chân đường cao hạ từ O đến AB. => OI = R.\(\dfrac{\sqrt{3}}{2}\).
Cos\(\widehat{IAO}\) = \(\dfrac{\sqrt{3}}{2}\)=> \(\widehat{A}\)= \(^{^{ }30^o}\). \(\widehat{OAB}=\widehat{HBA}\) (so le trong).
AH = Sin 30. AB = \(\dfrac{1}{2}.R.\sqrt{3}=R.\dfrac{\sqrt{3}}{2}\)
Vậy H cách A khoảng bằng \(\dfrac{\sqrt{3}}{2}\)

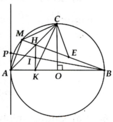
a, Chứng minh được H C B ^ = H K B ^ = 90 0
b, A C K ^ = H B K ^ (CBKH nội tiếp)
Lại có: A C M ^ = H B K ^ = 1 2 s đ A M ⏜
=> A C M ^ = A C K ^
c, Chứng minh được:
DMCA = DECB (c.g.c) => MC = CE
Ta có: C M B ^ = C A B ^ = 1 2 s đ C B ⏜ = 45 0
=> DMCE vuông cân tại C
d, Gọi P B ∩ H K = I
Chứng minh được DHKB đồng dạng với DAMB (g.g)
=> H K K B = M A M B = A P R => H K = A P . B K R
Mặt khác: ∆BIK:∆BPA(g.g) => (ĐPCM)