Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

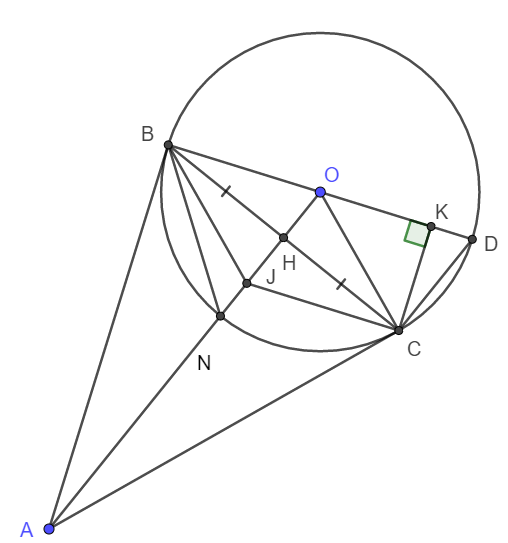
a) Tam giác vuông ABO và ACO có chung cạnh huyền AO nên O, B, A, C cùng thuộc đường tròn đường kính AO.
b) Theo tính chất hai tiếp tuyến cắt nhau, ta có AB = AC nên ABC là tam giác cân tại A.
Lại có AO là phân giác nên đồng thời là đường trung tuyến. Vậy thì AO đi qua H hay A, H, O thảng hàng.
Theo liên hệ giữa góc ở tâm và góc nội tiếp cùng chắn một cung, ta có \(\widehat{KDC}=\frac{\widehat{BOC}}{2}\)
Theo tính chất hai tiếp tuyến cắt nhau ta cũng có: \(\widehat{COA}=\frac{\widehat{BOC}}{2}\)
Suy ra \(\widehat{KDC}=\widehat{COA}\)
Vậy thì \(\Delta KDC\sim\Delta COA\left(g-g\right)\Rightarrow\frac{CK}{AC}=\frac{CD}{AO}\Rightarrow AC.CD=CK.AO\)
c) Ta thấy \(\widehat{ABN}=\widehat{NBC}\) (Góc nội tiếp và góc tạo bởi tiếp tuyến dây cung chắn các cung bằng nhau)
Vậy nên BN là phân giác góc ABC.
Lại có AN là phân giác góc BAC nên N là tâm đường tròn nội tiếp tam giác ABC.
d) Gọi J là trực tâm tam giác ABC. Ta có ngay \(JC\perp AB;BJ\perp AC\)
Vậy thì BO // JC ; BJ // OC
Suy ra tứ giác JBOC là hình bình hành.
Lại có OB = OC nên JBOC là hình thoi.
Từ đó ta có JB = JC = OB = OC = R.
Vậy khi A di chuyển trên tia By cố định thì BJ = R hay J thuộc đường tròn tâm B, bán kính R.

Bài 1:
a: Xét tứ giác BFEC có
\(\widehat{BFC}=\widehat{BEC}=90^0\)
Do đó: BFEC là tứ giác nội tiếp
c: Xét (O) có
ΔACD nội tiếp
AD là đường kính
Do đó: ΔACD vuông tại C
Xét (O) có
ΔABD nội tiếp
AD là đường kính
Do đó: ΔABD vuông tại B
Xét tứ giác BICD có
BI//CD(cùng vuông góc với AC)
CI//BD(cùng vuông góc với AB)
Do đó: BICD là hình bình hành
Bài 2:
a: Xét (O) có
MN=EF
OH là khoảng cách từ O đến dây MN
OK là khoảng cách từ O đến dây EF
Do đó: OH=OK
Xét ΔAHO vuông tại H và ΔAKO vuông tại K có
AO chung
OH=OK
Do đó: ΔAHO=ΔAKO
Suy ra: AH=AK
b: Xét ΔOHM vuông tại H và ΔOKE vuông tại K có
OM=OE
OH=OK
Do đó: ΔOHM=ΔOKE
Suy ra: HM=KE
Ta có: AM+MH=AH
AE+EK=AK
mà AH=AK
và HM=KE
nên AM=AE
a: góc AMO=góc AFO=góc ANO=90 độ
=>A,M,F,O,N cùng thuộc 1 đường tròn
b: Gọi I là giao của MN với AO
=>I là trung điểm của MN
AI*AO=AM^2
Xét ΔAMH và ΔAFM có
góc AMH=góc AFM
góc MAH chung
=>ΔAMH đồng dạng với ΔAFM
=>AH*AF=AI*AO
=>góc AHI=góc AOF
=>OFHI nội tiếp
=>M,N,H thẳng hàng