Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Để (d) cắt (d1) tại một điểm trên trục tung thì
\(\left\{{}\begin{matrix}m-2\ne2\\-2m+1=m+2\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}m\ne4\\-3m=1\end{matrix}\right.\Leftrightarrow m=-\dfrac{1}{3}\)
b: Tọa độ giao điểm của d1 và d2 là:
\(\left\{{}\begin{matrix}x+2=4-3x\\y=x+2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}4x=2\\y=x+2\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x=\dfrac{1}{2}\\y=\dfrac{1}{2}+2=\dfrac{5}{2}\end{matrix}\right.\)
Thay x=1/2 và y=5/2 vào (d), ta được:
\(\dfrac{1}{2}\left(m-2\right)+2+m=\dfrac{5}{2}\)
=>\(\dfrac{1}{2}m-1+m+2=\dfrac{5}{2}\)
=>\(\dfrac{3}{2}m=\dfrac{3}{2}\)
=>m=1
c: (d): y=(m-2)x+m+2
=mx-2x+m+2
=m(x+1)-2x+2
Tọa độ điểm cố định mà (d) luôn đi qua là:
\(\left\{{}\begin{matrix}x+1=0\\y=-2x+2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=-1\\y=-2\cdot\left(-1\right)+2=4\end{matrix}\right.\)

a: Khi m=1 thì (d): y=-x+3
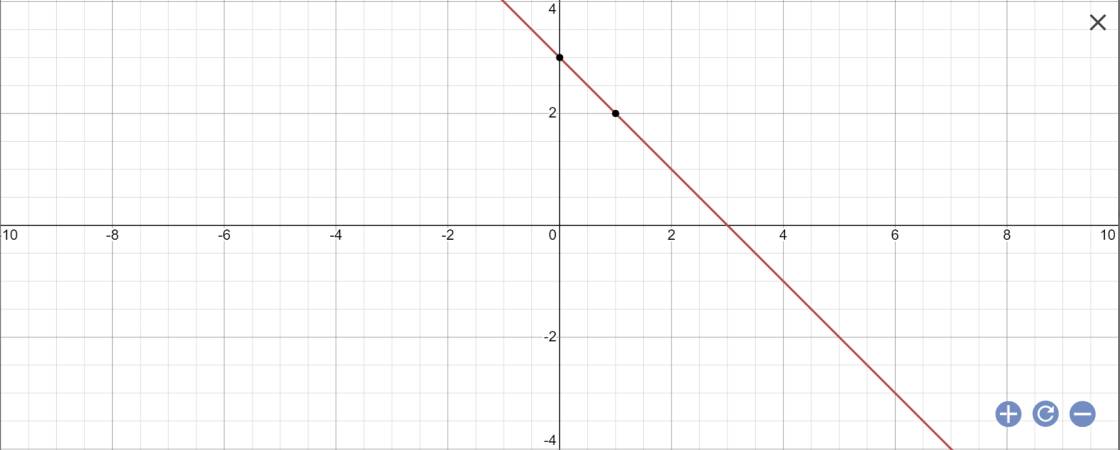
b: Tọa độ giao là:
4-3x=x+2 và y=x+2
=>-4x=-2 và y=x+2
=>x=1/2 và y=5/2
Thay x=1/2 và y=5/2 vào (d),ta được:
1/2(m-2)+m+2=5/2
=>1/2m-1+m+2=5/2
=>3/2m+1=5/2
=>m=1

a: Để hàm số y=(2m+3)x-2m+5 nghịch biến trên R thì 2m+3<0
=>2m<-3
=>\(m< -\dfrac{3}{2}\)
b: Để (d)//(d1) thì
\(\left\{{}\begin{matrix}2m+3=3m-2\\-2m+5\ne1\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}-m=-5\\-2m\ne-4\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}m=5\\m\ne2\end{matrix}\right.\)
=>m=5
c: Thay y=5 vào y=3x-1, ta được:
3x-1=5
=>3x=6
=>x=6/3=2
Thay x=2 và y=5 vào (d), ta được:
\(2\left(2m+3\right)-2m+5=5\)
=>\(4m+6-2m+5=5\)
=>2m+11=5
=>2m=-6
=>m=-6/2=-3
d: Tọa độ A là:
\(\left\{{}\begin{matrix}y=0\\\left(2m+3\right)x-2m+5=0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}y=0\\x\left(2m+3\right)=2m-5\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=0\\x=\dfrac{2m-5}{2m+3}\end{matrix}\right.\)
=>\(A\left(\dfrac{2m-5}{2m+3};0\right)\)
\(OA=\sqrt{\left(\dfrac{2m-5}{2m+3}-0\right)^2+\left(0-0\right)^2}=\sqrt{\left(\dfrac{2m-5}{2m+3}\right)^2}=\left|\dfrac{2m-5}{2m+3}\right|\)
Tọa độ B là:
\(\left\{{}\begin{matrix}x=0\\y=x\left(2m+3\right)-2m+5=0\left(2m+3\right)-2m+5=-2m+5\end{matrix}\right.\)
=>\(B\left(-2m+5;0\right)\)
\(OB=\sqrt{\left(-2m+5-0\right)^2+\left(0-0\right)^2}\)
\(=\sqrt{\left(-2m+5\right)^2}=\left|2m-5\right|\)
Vì Ox\(\perp\)Oy
nên OA\(\perp\)OB
=>ΔOAB vuông tại O
=>\(S_{OAB}=\dfrac{1}{2}\cdot\left|2m-5\right|\cdot\dfrac{\left|2m-5\right|}{\left|2m+3\right|}\)
\(=\dfrac{1}{2}\cdot\dfrac{\left(2m-5\right)^2}{\left|2m+3\right|}\)
Để \(S_{AOB}=1\) thì \(\dfrac{\dfrac{1}{2}\left(2m-5\right)^2}{\left|2m+3\right|}=1\)
=>\(\dfrac{\left(2m-5\right)^2}{\left|2m+3\right|}=2\)
=>\(\left(2m-5\right)^2=2\left|2m+3\right|\)
=>\(\left(2m-5\right)^2=2\left(2m+3\right)\)
=>\(4m^2-20m+25-4m-6=0\)
=>\(4m^2-24m+19=0\)
=>\(m=\dfrac{6\pm\sqrt{17}}{2}\)

a.
\(-2y+x-5=0\Leftrightarrow2y=x-5\Leftrightarrow y=\dfrac{1}{2}x-\dfrac{5}{2}\)
Hai đường thẳng cắt nhau khi:
\(m-2\ne\dfrac{1}{2}\Leftrightarrow m\ne\dfrac{5}{2}\)
b.
\(3x+y=1\Leftrightarrow y=-3x+1\)
Hai đường thẳng song song khi: \(\left\{{}\begin{matrix}m-2=-3\\n\ne1\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}m=-1\\n\ne1\end{matrix}\right.\)
c.
Hai đường thẳng trùng nhau khi:
\(\left\{{}\begin{matrix}m-2=2\\n=3\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}m=4\\n=3\end{matrix}\right.\)

a) để d2 // d3 => 3 = 2m -3 <=> 6 = 2m => m = 3
b) để d2 cắt d3 => 2m -3 ≠ 3 <=> 2m ≠ 6 => m ≠ 3
c) để d1 ⊥ d3 => 2 . ( 2m -3 ) = -1 <=> 4m -6 = 1 <=> 4m = 7 => m = 7/4

a: Để (d)//(d1) thì \(\left\{{}\begin{matrix}m^2+2m=-1\\m+1\ne-2023\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}m^2+2m+1=0\\m\ne-2024\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}\left(m+1\right)^2=0\\m\ne-2024\end{matrix}\right.\)
=>(m+1)2=0
=>m+1=0
=>m=-1
b: Thay x=0 và y=2024 vào (d), ta được:
\(0\left(m^2+2m\right)+m+1=2024\)
=>m+1=2024
=>m=2023
c: Tọa độ giao điểm của (d2) và (d3) là:
\(\left\{{}\begin{matrix}x-2=-4x+3\\y=x-2\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}5x=5\\y=x-2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=1\\y=1-2=-1\end{matrix}\right.\)
Thay x=1 và y=-1 vào (d), ta được:
\(1\left(m^2+2m\right)+m+1=-1\)
=>\(m^2+3m+2=0\)
=>(m+2)(m+1)=0
=>\(\left[{}\begin{matrix}m+2=0\\m+1=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}m=-2\\m=-1\end{matrix}\right.\)

Ta biết đổi lại thành \(y\left(2m-2\right)=\left(m+3\right)-\left(m-1\right)x\)
a/ Để đths song song với (d) : \(y=\frac{3x-1}{2}=\frac{3}{2}x-\frac{1}{2}\)thì \(\begin{cases}2m-2\ne0\\m+3\ne-\frac{1}{2}\\-\left(m-1\right)=\frac{3}{2}\end{cases}\) \(\Leftrightarrow m=-\frac{1}{2}\) (thỏa mãn)
Còn lại tương tự.
b/ Gọi điểm cố định là \(N\left(x_0;y_0\right)\)
Vì đths đi qua N nên \(\left(m-1\right)x_0+\left(2m-2\right)y_0=m+3\Leftrightarrow m\left(x_0+2y_0-1\right)-\left(x_0+2y_0+3\right)=0\)
Để N là điểm cố định thỏa mãn thì
\(\begin{cases}x_0+2y_0-1=0\\x_0+2y_0+3=0\end{cases}\) . Hệ này vô nghiệm.
Vậy không có điểm cố định.
a: Tọa độ giao điểm của đường thẳng (d1) và đường thẳng (d2) là:
\(\left\{{}\begin{matrix}3x-1=2x+1\\y=2x+1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}3x-2x=2+1\\y=2x+1\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x=3\\y=2\cdot3+1=7\end{matrix}\right.\)
Thay x=3 và y=7 vào (d), ta được:
\(3\left(4m+5\right)-2m+7=7\)
=>\(12m+15-2m=0\)
=>10m=-15
=>m=-3/2
b: để (d)//(d3) thì \(\left\{{}\begin{matrix}4m+5=-3\\-2m+7< >2\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}4m=-3-5=-8\\-2m< >-5\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}m=-2\\m< >\dfrac{5}{2}\end{matrix}\right.\)
=>m=-2