Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Câu 1: AB=2 cm, D là trung điểm, suy ra AD=DB=1 cm. B là trung điểm DE, suy ra DB=BE=1 cm.
Câu 2: Tương tự như trên, ta suy ra DE=DB+BE=1+1=2 (cm).

Do I là trung điểm của AB nên: I A → + I B → = 0 → hay I B → = − I A →
M A → . M B → = M I → + I A → . M I → + I B → = M I → 2 + I A → + I B → . M I → + I A → . I B → .
= ( M I ) ⃗ 2 + 0 ⃗ . ( M I ) ⃗ + ( I A ) ⃗ . ( - ( I A ) ⃗ ) = 〖 M I 〗 2 - 〖 I A 〗 2
Chọn B.

a: OB=10-3=7cm
=>OB>BM
=>M nằm giữa O và B
b: OM=AM-AO=2cm

Bài 2:
a: Vì AM<ÂN
nên điểm M nằm giữa hai điểm A và N
b: MN=AN-AM=5cm
c: PM=PA+AM=3+2=5cm
d: VìMP=MN
và P,M,N thẳng hàng
nên M là trung điểm của PN

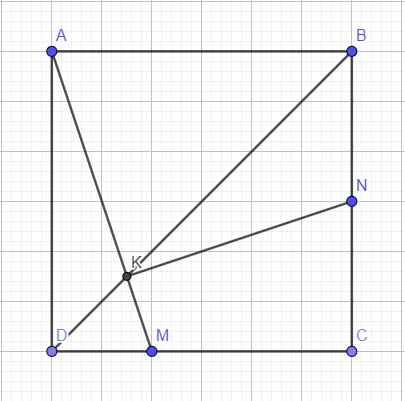
Talet: \(\dfrac{KM}{AK}=\dfrac{DM}{AB}=\dfrac{1}{3}\Rightarrow KM=\dfrac{1}{3}AK\Rightarrow KM=\dfrac{1}{4}AM\Rightarrow\overrightarrow{KM}=\dfrac{1}{4}\overrightarrow{AM}\)
Mà \(\overrightarrow{AM}=\overrightarrow{AD}+\overrightarrow{DM}=\overrightarrow{AD}+\dfrac{1}{3}\overrightarrow{AB}\Rightarrow\overrightarrow{KM}=\dfrac{1}{4}\overrightarrow{AD}+\dfrac{1}{12}\overrightarrow{AB}\)
\(\overrightarrow{KN}=\overrightarrow{KM}+\overrightarrow{MC}+\overrightarrow{CN}=\dfrac{1}{4}\overrightarrow{AD}+\dfrac{1}{12}\overrightarrow{AB}+\dfrac{2}{3}\overrightarrow{AB}-\dfrac{1}{2}\overrightarrow{AD}\)
\(=\dfrac{3}{4}\overrightarrow{AB}-\dfrac{1}{4}\overrightarrow{AD}\)
\(\Rightarrow\overrightarrow{AM}.\overrightarrow{KN}=\left(\overrightarrow{AD}+\dfrac{1}{3}\overrightarrow{AB}\right)\left(\dfrac{3}{4}\overrightarrow{AB}-\dfrac{1}{4}\overrightarrow{AD}\right)=\dfrac{1}{4}AB^2-\dfrac{1}{4}AD^2=0\)
\(\Rightarrow AM\perp KN\Rightarrow\) đường thẳng KN nhận (10;1) là 1 vtpt
Phương trình NK:
\(10\left(x-0\right)+1\left(y-2019\right)=0\Leftrightarrow10x+y-2019=0\)
\(d\left(O;NK\right)=\dfrac{\left|-2019\right|}{\sqrt{10^2+1^2}}=\dfrac{2019}{\sqrt{101}}\)

Gọi giao của d và AB là C
=>C là trung điểm của AB và MC=4cm
=>CA=CB=AB/2=3cm
\(MA=MB=\sqrt{3^2+4^2}=5\left(cm\right)\)
IM=IN=MN/2=5(cm)
=>KI=2MI=10(cm)
=>KN=15(cm)