Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

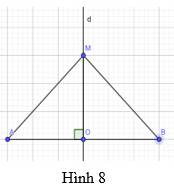
Gọi giao của d và AB là C
=>C là trung điểm của AB và MC=4cm
=>CA=CB=AB/2=3cm
\(MA=MB=\sqrt{3^2+4^2}=5\left(cm\right)\)

M A B H d
H là trung điểm AB nên AH = BH
d vuông góc với AB \(\Rightarrow\widehat{MHA}=\widehat{MHB}=90^o\)
Xét tam giác AHM và tam giác BHM có :
AH = HB
\(\widehat{MHA}=\widehat{HBM}=90^o\)
MH là cạnh chung
\(\Rightarrow\Delta AHM=\Delta MHB\)
\(\Rightarrow MA=MB\)
Chúc bạn học tốt !!!

xét tam giác amh và tam giác bmh có
ah = hb (gt)
góc ahm = góc bhm (=90 độ)
mh chung
=> tam giác amh = tam giác bmh (c.g.c)

Gọi giao điểm của 2 đoạn thẳng AB và đg trung trực là H
HA=HB=3 cm
Xét tam giác vuông AHM , ta có
AM2= AH2+MH2 ( định lý py-ta-go)
hay AM2= 32+42= 9 +16= 25
=> AM=\(\sqrt{25}\)=5 cm
mà MA=MB (gt)
=> MA=MB=5cm
Chúc bạn học tốt

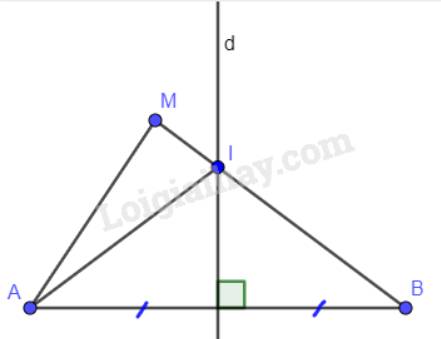
a) Ta có: Đường thẳng d là đường trung trực của đoạn thẳng AB. Mà điểm I thuộc đường thẳng d nên suy ra: IA = IB. (Một điểm thuộc đường trung trực thì cách đều hai đầu mút).
Ta có: \(MB = MI + IB\) mà IA = IB nên \(MB = MI + IA = AI + IM\).
b) Xét tam giác AMI có: \(MA < AI + IM\)(Tổng hai cạnh bất kì trong một tam giác luôn lớn hơn độ dài cạnh còn lại) mà \(MB = AI + IM\).
Vậy \(MA < MB\).

bạn xem link này nhé mình vừa làm xong :
https://olm.vn/hoi-dap/detail/228037897085.html

Gọi trung điểm của AB là I
Ta có tam giác AMI vuông tại I. Theo định lý Pytago ta có
IM2 = AM2 - AI2 = 62 - 42 = 20 ⇒ IM = 20 c m . Chọn C

a: AC=8cm
Xét ΔCBD có
CA là đường cao
CA là đường trung tuyến
Do đó: ΔCBD cân tại C
hay CB=CD
Xét ΔCBD có
DK là đường trung tuyến
CA là đường trung tuyến
DK cắt CA tại M
Do đó: M là trọng tâm
=>AM=AC/2=8/3(cm)
b: Xét ΔCAD có
G là trung điểm của AC
GQ//AD
Do đó: Q là trung điểm của CD
Vì M là trọng tâm của ΔCDB nên B,M,Q thẳng hàng

Vì M thuộc trung trực của AB \( \Rightarrow \) MA = MB \( \Rightarrow \) 7 = x + 2 \( \Rightarrow \) x = 5