Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án C
Xét pt tương giao:
2 x - 1 x - 1 = x + m ⇔ 2 x - 1 - x + m x - 1 = 0 ⇔ x 2 - 3 - m x + m - 1 = 0
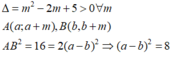
a + b 2 - 4 a b = 8 ⇔ 3 - m 2 - 4 1 - m = 8 ⇔ [ m = - 1 m = 3

Chọn C.
Phương pháp: Sử dụng phương trình hoành độ giao điểm và định lý Viet.
Cách giải: Phương trình hoành độ giao điểm là

Vì a,c là nghiệm của (*) nên theo định lý Viet ta có:
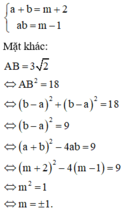

Đường thẳng AC qua A ( -2;3 ); C ( 4;1 ) nhận A C → = 6 ; - 2 làm vec tơ chỉ phương nên có phương trình là: x + 2 6 = y - 3 - 2 ⇔ y = - 1 3 x + 7 3
Tọa độ giao điểm của AC và BD là nghiệm của hệ phương trình 3 x - y - 1 = 0 y = - 1 3 x + 7 3 ⇔ x = 1 y = 2
Để ý rằng A C ⊥ B D và I là trung điểm AC.
Khi đó ABCD là hình thoi thì I ( 1;2 ) là trung điểm của BD.
Phương trình hoành độ giao điểm của (C) và d là: 2 x + 1 2 x - m = 3 x - 1 ⇔ 6 x 2 - 3 m + 4 x + m - 1 = 0
Do ∆ = 3 m + 4 2 - 4 . 6 m - 1 = 9 m 2 + 24 > 0 , ∀ m nên d luôn cắt (C) tại hai điểm phân biệt B và D.
Gọi x 1 , x 2 là hai nghiệm của phương trình (*). Theo định lý Viet ta có x 1 + x 2 2 = 3 m + 4 12
Đáp án A
Để I là trung điểm của BD thì 3 m + 4 12 = 1 ⇔ m = 8 3
Đáp án A

Phương trình hoành độ giao điểm của (C) và d là:
x + 1 x - 1 = 2 x + m ⇔ x ≠ 1 f x = 2 x 2 + m - 3 - m - 1
Ta có
∆ = m 2 + 2 m + 7 > 0 ∀ m f 1 = - 2 ≠ 0
=> d luôn cắt ![]() tại hai điểm phân biệt A, B.
tại hai điểm phân biệt A, B.
Gọi x 1 ; x 2 lần lượt là hoành độ các điểm A, B. Khi đó A O B ⏞ nhọn.
⇔ cos A O B ⏞ = O A 2 + O B 2 - A B 2 2 . O A . O B > 0 ⇔ O A 2 + O B 2 > A B 2 ⇔ x 1 2 + 2 x 1 + m 2 + x 2 2 + 2 x 2 + m 2 > 5 x 2 - x 1 2
Sử dụng định lí Viet và giải bất phương trình theo m ta thu được m > 5
Đáp án C

Đáp án C.
Phương trình có hoành độ giao điểm của d và (C):
x 3 + 2 m x 2 + ( m + 3 ) x + 4 = x + 4 ⇔ x 2 + 2 m x + ( m + 2 ) = 0
Để d cắt (C) tại 3 điểm phân biệt A(0;4) và C thì phương trình (*) phải có hai nghiệm phân biệt x 1 , x 2 khác 0
⇔ 0 2 + 2 m . 0 + m + 2 ≢ 0 ∆ ' = m 2 - m - 2 > 0 ⇔ m + 2 ≢ 0 ( m + 1 ) ( m - 2 ) > 0 ⇔ m ≢ - 2 m > 2 m < - 1 ⇔ m > 2 m < - 1 m ≢ - 2 (1)
Giả sử B x 1 ; x 1 + 4 và B x 2 ; x 2 + 4 với x 1 , x 2 là hai nghiệm của (*)
Suy ra B C = 2 x 1 - x 2 và theo định lí Vi-ét: x 1 + x 2 = - 2 m x 1 x 2 = m + 2
Ta có S ∆ M B C = 1 2 d ( M ; B C ) . B C = 1 2 . 1 - 3 + 4 2 . 2 x 1 - x 2 = x 1 - x 2
Từ giả thiết ta có S ∆ M B C = 4 ⇔ x 1 - x 2 = 4 ⇔ x 1 - x 2 2 = 16
⇔ x 1 + x 2 2 - 4 x 1 x 2 = 16 ⇔ ( - 2 m ) 2 - 4 ( m + 2 ) - 16 = 0 ⇔ 4 m 2 - 4 m - 24 = 0
m = - 2 m = 3 . Đối chiếu với điều kiện (1), chỉ có m = 3 là thỏa mãn
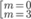
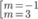


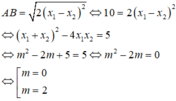


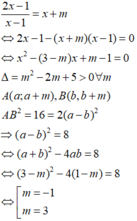
Đáp án C.
Ta xét phương trình:
x x − 1 = − x + m ⇔ x 2 − m x + m = 0 .
Ta cần điều kiện để phương trình này có 2 nghiệm phân biệt
⇔ Δ = m 2 − 4 m > 0 ⇔ m ∈ − ∞ ; 0 ∪ 4 ; + ∞ .