Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn A.
Với M (a,b,c) thì hình chiếu vuông góc của M lên mặt phẳng (Oxy) là M1(a;b;0)
Do đó, hình chiếu của điểm M(1;2;-3) lên mặt phẳng (Oxy) là điểm M’(1;2;0).

Gọi tọa độ M(x;y;z)
Ta có: \(\overrightarrow{AB}\) = (2; -2; -8)
\(\overrightarrow{AM}\)=( x+1; y-2; z-3)
A, B, M thẳng hàng khi: \(\left[\overrightarrow{AB};\overrightarrow{AM}\right]\)=\(\overrightarrow{0}\) ⇔ \(\left\{{}\begin{matrix}-2z+8y-10=0\\-8x-2z-2=0\\2y+2x-2=0\end{matrix}\right.\)
⇔\(\left\{{}\begin{matrix}x=0\\y=1\\z=-1\end{matrix}\right.\)
=> Câu D đúng

Chọn D
Ta có x + my + (2m + 1)z – m – 2 = 0 <=> m(y + 2z -1) + x + z - 2 = 0 (*)
Phương trình (*) có nghiệm với 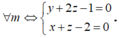
Suy ra (P) luôn đi qua đường thẳng 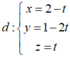
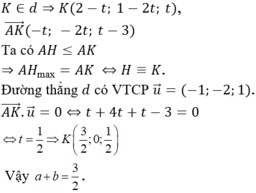

Đáp án A
Phương pháp:
Hình chiếu vuông góc của điểm M ( x 0 ; y 0 ; z 0 ) trên mặt phẳng (Oxy) là điểm M ' ( x 0 ; y 0 ; z 0 )
Cách giải:
Hình chiếu vuông góc của điểm A(1;2;3) trên mặt phẳng (Oxy) là điểm N(1;2;0)

Đáp án C
Hình chiếu vuông góc của M(2;-1;4) lên mặt phẳng (Oxy) là điểm H(2;-1;0).

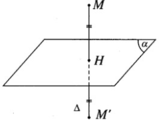
Phương trình tham số của đường thẳng ∆ đi qua điểm M(1; -1; 2) và vuông góc với mặt phẳng ( α ): 2x – y + 2z + 12 = 0 là:
Δ 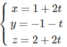
Xét điểm H(1 + 2t; -1 – t; 2 + 2t) ∈ ∆
Ta có H ∈ ( α ) ⇔ 2(1 + 2t) + (1 + t) + 2(2 + 2t) + 12 = 0 ⇔ t = −19/9
Vậy ta được ![]()

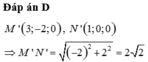
Chọn A.
Với M(a, b, c) thì hình chiếu vuông góc của M lên mặt phẳng (Oxy) là M_1(a;b;0)
Do đó,hình chiếu của điểm M(1;2;-3) lên mặt phẳng (Oxy) là điểm M’(1;2;0).