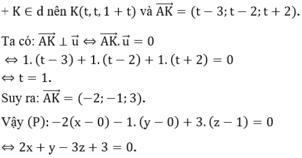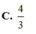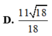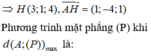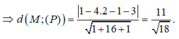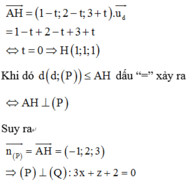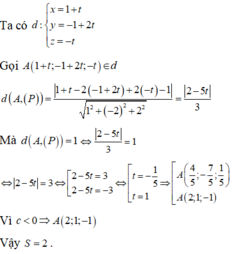Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Đáp án là D.
Ta có:
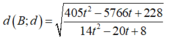
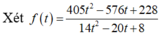
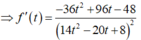
Đường thẳng d đi qua A(1;2;-1) và có VTCP
Có hai trường hợp xảy ra:
Trường hợp 1:
(P) đi qua A, song song với hai đường thẳng d và BC. Vectơ chỉ phương của d là v → (-3; -1; 2) và BC → (-2; 4; 0).
Do đó n P → = v → ∧ BC → = (-8; -4; -14).
Phương trình mặt phẳng (P) là: -8(x - 1) - 4(y - 2) - 14(z - 1) = 0 hay 4x + 2y + 7z - 15 = 0
Trường hợp 2:
(P) đi qua A, đi qua trung điểm F(1; 1; 1) của BC, và song song với d.
Ta có: FA → (0; 1; 0), FA → ∧ v → = (2; 0; 3).
Suy ra phương trình của (P) là: 2(x - 1) + 3(z - 1) = 0 hay 2x + 3z - 5 = 0.
Chọn D
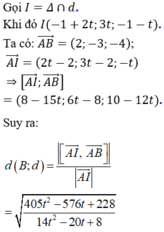
Xét hàm số:
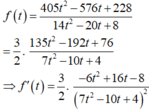
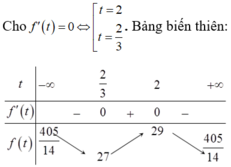
Do đó d (B; d) nhỏ nhất khi f(t) đạt giá trị nhỏ nhất bằng 27 tại t = 2/3. Suy ra 
. Chọn một vectơ chỉ phương của đường thẳng d là 
Vậy phương trình đường thẳng 
Chọn A
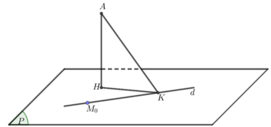
+ d qua M0 (0;0;1) có vectơ chỉ phương 
+ Gọi H, K lần lượt là hình chiếu của A lên (P) và d. Ta có: d(A, (P)) = AH ≤ AK
Đẳng thức xảy ra khi và chỉ khi H ≡ K. Do đó d(A, (P))max = AK
Khi đó (P) đi M0 (0;0;1) nhận 
làm vectơ pháp tuyến.
