Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

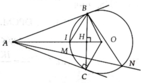
a, A B M ^ = A N B ^ = 1 2 s đ B M ⏜
Chứng minh được: ∆ABM:∆ANB (g.g) => ĐPCM
b, Chứng minh AO ^ BC áp dụng hệ thức lượng trong tam giác vuông ABO và sử dụng kết quả câu a) Þ AB2 = AH.AO
c, Chứng minh được A B I ^ = C B I ^ B I ⏜ = C I ⏜ => BI là phân giác A B C ^ . Mà AO là tia phân giác B A C ^ => I là tâm đường tròn nội tiếp ∆ABC

a: góc ABO+góc ACO=90+90=180 độ
=>ABOC nội tiếp đường tròn đường kính OA
Tâm là trung điểm của OA
Bán kính là OA/2
b: Xét (O) có
AB,AC là tiếp tuyến
=>AB=AC
mà OB=OC
nên OA là trung trực của BC
=>AO vuông góc BC
c: Xét ΔAMB và ΔABN có
góc AMB=góc ABN
góc MAB chung
=>ΔAMB đồng dạng với ΔABN
=>AM/AB=AB/AN
=>AB^2=AM*AN=AH*AO


a, A,H,O thẳng hàng vì AH,AO cùng vuông góc với BC
HS tự chứng minh A,B,C,O cùng thuộc đường tròn đường kính OA
b, Ta có K D C ^ = A O D ^ (cùng phụ với góc O B C ^ )
=> ∆KDC:∆COA (g.g) => AC.CD = CK.AO
c, Ta có: M B A ^ = 90 0 - O B M ^ và M B C ^ = 90 0 - O M B ^
Mà O M B ^ = O B M ^ (∆OBM cân) => M B A ^ = M B C ^
=> MB là phân giác A B C ^ . Mặt khác AM là phân giác B A C ^
Từ đó suy ra M là tâm đường tròn nội tiếp tam giác ABC
d, Kẻ CD ∩ AC = P. Chứng minh ∆ACP cân tại A
=> CA = AB = AP => A là trung điểm CK

a. Ta có: \(\Lambda\)ABO=90 ( do AB là tiếp tuyến của (O))
\(\Lambda\)ACO=90 ( do AC là tiếp tuyến của (O))
\(\Rightarrow\) \(\Lambda\)ABO + \(\Lambda\)ACO = 90 + 90 = 180.
Suy ra: tứ giác ABOC nội tiếp.
b. Ta có: AB,AC lần lượt là tiếp tuyến của (O) nên AB=AC.
\(\Rightarrow\)\(\Delta\)ABC cân tại A lại có AH là tia phân giác nên AH cũng là đường cao
\(\Rightarrow\)AO\(\perp\)BC tại H.
Áp dụng đinh lý Py-ta-go vào \(\Delta\)ABO ta có:
AO2 = AB2 + BO2 = 42 + 32 = 25
\(\Rightarrow\)AO = 5 (cm).
Áp dụng hệ thức giữa cạnh và đường cao trong tam giác vuông ABO ta được:
AB2 = AH.AO \(\Rightarrow\) AH = \(\dfrac{AB^2}{AO}\)=\(\dfrac{16}{5}\)(cm)
c. Ta có: \(\Lambda\)ACE=\(\Lambda\)ADC ( tính chất của góc tạo bởi tia tiếp tuyến và dây cung )
Xét \(\Delta\)ACE và \(\Delta\)ADC có:
\(\Lambda ACE=\Lambda ADC\)
\(\Lambda\)CAD chung
Do đó: \(\Delta ACE\sim\Delta ADC\) \(\Rightarrow\dfrac{AC}{AD}=\dfrac{AE}{AC}\) \(\Rightarrow\)AC2 = AD.AE (1)
Áp dụng hệ thức giữa cạnh và đường cao trong tam giác vuông ACO có:
AC2 = AH.AO (2)
Từ (1) và (2) ,suy ra: AD.AE = AH.AO.
a)Ta có:\(\widehat{ABO};\widehat{ACO}\) lần lượt là góc nội tiếp chắn nửa đường tròn
\(\Rightarrow\widehat{ABO=}\widehat{ACO}=90^{ }\)
\(\Rightarrow\widehat{ABO}+\widehat{ACO}=90+90=180\)
Mà hai góc này đối nhau nên tứ giác ABOC nội tiếb)
b)Theo a) ta có:\(\widehat{ABO}=90\)⇒▲ABO là tam giác vuông tại B đường cao AH.
Áp dụng định lí pytago vào tam giác vuông ABO đường cao AH ta có:
\(AO^2=AB^2+BO^2=4^2+3^2=25\)
\(\Rightarrow\sqrt{AO}=5\) cm.
Áp dụng hệ thức lượng giữa cạnh và đường cao trong ▲vuông ABO ta có:
\(AB^2=AH\cdot AO\)
\(\Rightarrow AH=\dfrac{AB^2^{ }}{AO}=\dfrac{4^2^{ }}{5}=\dfrac{16}{5}\)
a) Do AB là tiếp tuyến của (O) tại B nên \(\widehat{ABO}=90^o\). CMTT, ta có \(\widehat{ACO}=90^o\) \(\Rightarrow\widehat{ABO}+\widehat{ACO}=180^o\) \(\Rightarrow\) Tứ giác ABOC nội tiếp (đpcm).
b) Theo tính chất 2 tiếp tuyến cắt nhau, ta có \(AO\perp BC\). Tam giác ABO vuông tại B, có đường cao BH nên \(AB^2=AH.AO\)
Mặt khác, lại có \(\widehat{ABD}=\widehat{ACB}\) (góc tạo bởi tiếp tuyến và dây cung và góc nội tiếp cùng chắn cung đó) nên \(\Delta ABD~\Delta AEB\left(g.g\right)\) \(\Rightarrow\dfrac{AB}{AE}=\dfrac{AD}{AB}\) \(\Rightarrow AB^2=AD.AE\)
Từ đó dễ dàng suy ra \(AD.AE=AH.AO\)
c) Do tính chất của 2 tiếp tuyến cắt nhau nên \(\left\{{}\begin{matrix}MD=MB\\ND=NC\end{matrix}\right.\)
Do đó \(C_{AMN}=AM+AN+MN\)
\(=AM+AN+\left(MD+ND\right)\)
\(=\left(AM+MD\right)+\left(AN+ND\right)\)
\(=\left(AM+MB\right)+\left(AN+NC\right)\)
\(=AB+AC\)
\(=2AB\)
Lại có \(AB=\sqrt{AO^2-R^2}=\sqrt{6^2-3,6^2}=4,8cm\)
\(\Rightarrow C_{AMN}=2AB=2.4,8=9,6cm\)
k biết