Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

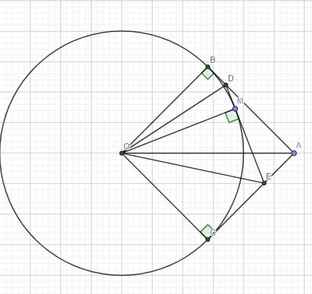
Cho điểm A nằm ngoài đường tròn (O;R) và OA = 2R. Vẽ các tiếp tuyến AB, AC với đường tròn (O) [B, C∈(O)]. Khẳng định nào sau đây đúng?
A. AB=AC=BC2=R3
B.AB=AC=BC=R5
C. AB=AC=BC=R3
D.

Do AB là tiếp tuyến \(\Rightarrow\Delta OAB\) vuông tại A
Theo định lý Pitago:
\(AB=\sqrt{OA^2-OB^2}=\sqrt{2R^2-R^2}=R\)
\(\Rightarrow AB=OB\Rightarrow\Delta OAB\) vuông cân tại B
Hoàn toàn tương tự ta có tam giác \(OAC\) vuông cân tại C
\(\Rightarrow OBAC\) là hình vuông
b.
Do DB và DM là 2 tiếp tuyến \(\Rightarrow DB=DM\)
Tương tự ta có \(EM=EC\)
\(\Rightarrow\) Chu vi tứ giác ADE:
\(AD+DE+EA=AD+DM+ME+EA=AD+DB+EC+EA=AB+AC=2R\)

a: Xét tứ giác ABOC có
\(\widehat{OBA}+\widehat{OCA}=90^0+90^0=180^0\)
=>ABOC là tứ giác nội tiếp
=>A,B,O,C cùng thuộc một đường tròn
b: Xét (O) có
AB,AC là tiếp tuyến
Do đó: AB=AC và AO là phân giác của góc BAC
Ta có: AB=AC
=>A nằm trên đường trung trực của BC(1)
Ta có: OB=OC
=>O nằm trên đường trung trực của BC(2)
từ (1) và (2) suy ra AO là đường trung trực của BC
=>OA\(\perp\)BC
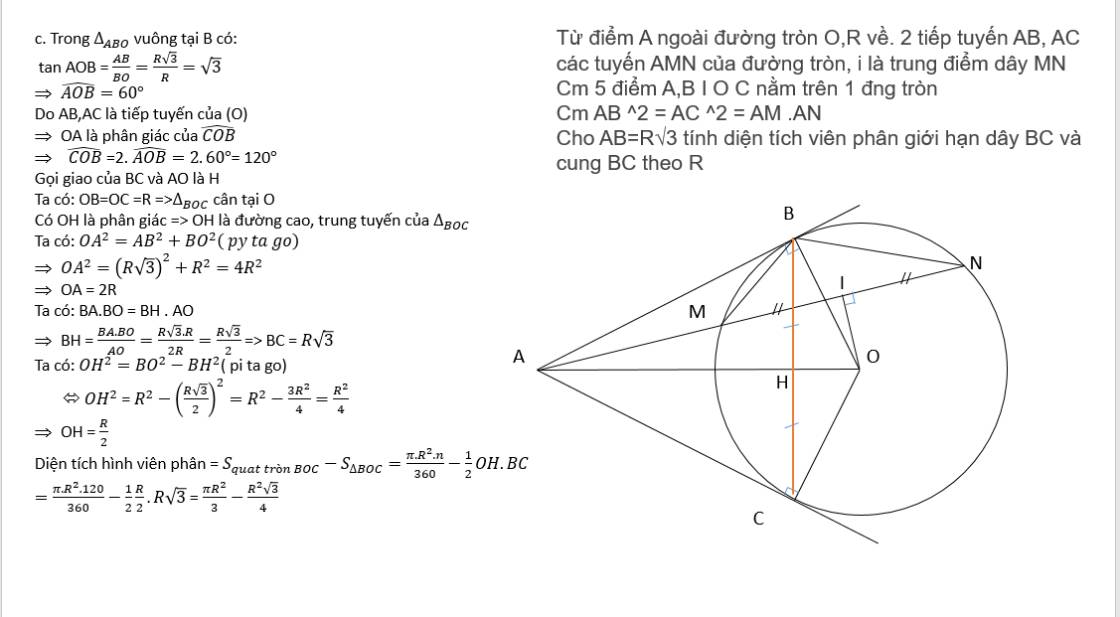
c: Xét ΔOBA vuông tại B có \(sinBAO=\dfrac{OB}{OA}=\dfrac{1}{2}\)
nên \(\widehat{BAO}=30^0\)
Ta có: AO là phân giác của góc BAC
=>\(\widehat{BAC}=2\cdot\widehat{BAO}=60^0\)
Ta có: ΔOBA vuông tại B
=>\(BO^2+BA^2=OA^2\)
=>\(BA^2=\left(2R\right)^2-R^2=3R^2\)
=>\(BA=R\sqrt{3}\)
Xét ΔBAC có AB=AC và \(\widehat{BAC}=60^0\)
nên ΔBAC đều
=>\(S_{BAC}=\dfrac{BA^2\cdot\sqrt{3}}{4}=\dfrac{3R^2\cdot\sqrt{3}}{4}\)

lớp 9 làm quen không bạn ^^