Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xét ΔABC có
\(\widehat{A}+\widehat{B}+\widehat{C}=180^0\)
=>\(\widehat{A}=180^0-75^0-45^0=60^0\)
Xét ΔABC có
\(\dfrac{AB}{sinC}=\dfrac{BC}{sinA}\)
=>\(\dfrac{AB}{sin45}=\dfrac{50}{sin60}\)
=>\(AB\simeq40,82\)
b: \(S_{ABC}=\dfrac{1}{2}\cdot BA\cdot BC\cdot sinABC=\dfrac{1}{2}\cdot40,82\cdot50\cdot sin75\simeq985,73\)
c: Độ dài đường cao xuất phát từ A là:
\(2\cdot\dfrac{985.73}{50}=39,4292\left(\right)\)

1.
\(\overrightarrow{AD}=\overrightarrow{AB}+\overrightarrow{BD}=\overrightarrow{AB}+\dfrac{c}{b+c}\overrightarrow{BC}=\dfrac{\left(b+c\right)\overrightarrow{AB}+c\overrightarrow{BC}}{b+c}=\dfrac{b\overrightarrow{AB}+c\overrightarrow{AC}}{b+c}\)
\(\Rightarrow AD^2=\dfrac{\left(b\overrightarrow{AB}+c\overrightarrow{AC}\right)^2}{\left(b+c\right)^2}=\dfrac{2b^2c^2+2b^2c^2.cosA}{\left(b+c\right)^2}=\dfrac{2b^2c^2\left(1+cos\alpha\right)}{\left(b+c\right)^2}\)
\(\Rightarrow AD=\dfrac{bc\sqrt{2+2cos\alpha}}{b+c}\)
2.
\(MA^2+MB^2+MC^2=\left(\overrightarrow{MG}+\overrightarrow{GA}\right)^2+\left(\overrightarrow{MG}+\overrightarrow{GB}\right)^2+\left(\overrightarrow{MG}+\overrightarrow{GC}\right)^2\)
\(=3MG^2+GA^2+GB^2+GC^2+2\overrightarrow{MG}\left(\overrightarrow{GA}+\overrightarrow{GB}+\overrightarrow{GC}\right)\)
\(=3MG^2+GA^2+GB^2+GC^2\)
\(=3MG^2+\dfrac{4}{9}\left(AM^2+MB^2+MC^2\right)\)
\(=3MG^2+\dfrac{4}{9}\left(\dfrac{2b^2+2c^2-a^2}{4}+\dfrac{2a^2+2c^2-b^2}{4}+\dfrac{2a^2+2b^2-c^2}{4}\right)\)
\(=3MG^2+\dfrac{4}{9}.\dfrac{3}{4}\left(a^2+b^2+c^2\right)\)
\(=3MG^2+\dfrac{1}{3}\left(a^2+b^2+c^2\right)\)

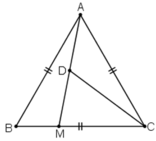
a) Do tam giác ABC là tam giác đều nên 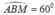 .
.
Theo định lý côsin trong tam giác ABM ta có:

b) Theo định lý sin trong tam giác ABM ta có:
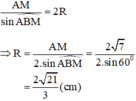
c) Ta có: BM + MC = BC nên MC = BC – BM = 6 - 2 = 4 cm.
Gọi D là trung điểm AM.
Áp dụng công thức độ dài đường trung tuyến trong tam giác ta có:
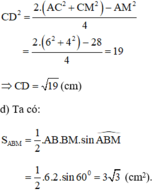

\(\widehat{B}=180^o-60^o-45^o=75^o\)
Theo định lý sin ta có:
\(\dfrac{AB}{sinC}=\dfrac{AC}{sinB}\)
\(\Rightarrow AC=\dfrac{AB\cdot sinB}{sinC}=\dfrac{5\cdot sin75^o}{sin45^o}=\dfrac{5+5\sqrt{3}}{2}\)
Mà: \(S_{ABC}=\dfrac{1}{2}\cdot AB\cdot AC\cdot sinA\)
\(\Rightarrow S_{ABC}=\dfrac{1}{2}\cdot5\cdot\dfrac{5+5\sqrt{3}}{2}\cdot sin60^o=\dfrac{75+25\sqrt{3}}{8}\left(dvdt\right)\)

a) Ta có:
\(\widehat{A}=180^o-60^o-45^o=75^o\)
Áp dụng định lý sin ta có:
\(\dfrac{BC}{sinA}=\dfrac{AC}{sinB}\)
\(\Rightarrow AC=\dfrac{BC\cdot sinB}{sinA}\)
\(\Rightarrow AC=\dfrac{a\cdot sin60^o}{sin75^o}=a\cdot\dfrac{3\sqrt{2}-\sqrt{6}}{2}\)
\(\dfrac{BC}{sinA}=\dfrac{AB}{sinC}\)
\(\Rightarrow AB=\dfrac{BC\cdot sinC}{sinA}\)
\(\Rightarrow AB=\dfrac{a\cdot sin45^o}{sin75^o}=a\cdot\left(\sqrt{3}-1\right)\)
b) \(cos75^o\)
\(=cos\left(30^o+45^o\right)\)
\(=cos30^o\cdot cos45^o-sin30^o\cdot sin45^o\)
\(=\dfrac{\sqrt{3}}{2}\cdot\dfrac{\sqrt{2}}{2}-\dfrac{1}{2}\cdot\dfrac{\sqrt{2}}{2}\)
\(=\dfrac{\sqrt{2}}{2}\cdot\left(\dfrac{\sqrt{3}-1}{2}\right)\)
\(=\dfrac{\sqrt{6}-\sqrt{2}}{4}\left(dpcm\right)\)
Bạn xem lại đề nhé, còn thiếu dữ kiện gì nhé