Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a.
\(\overrightarrow{AM}+\overrightarrow{BC}=\overrightarrow{AC}+\overrightarrow{CM}+\overrightarrow{BM}+\overrightarrow{MC}=\overrightarrow{AC}+\overrightarrow{BM}\)
b.
\(\overrightarrow{AE}=3\overrightarrow{EM}=3\overrightarrow{EA}+3\overrightarrow{AM}\Rightarrow4\overrightarrow{AE}=3\overrightarrow{AM}\Rightarrow\overrightarrow{AE}=\dfrac{3}{4}\overrightarrow{AM}\)
\(\Rightarrow\overrightarrow{AE}=\dfrac{3}{4}\left(\dfrac{1}{2}\overrightarrow{AB}+\dfrac{1}{2}\overrightarrow{AC}\right)=\dfrac{3}{8}\overrightarrow{AB}+\dfrac{3}{8}\overrightarrow{AC}\)
\(\overrightarrow{BE}=\overrightarrow{BA}+\overrightarrow{AE}=-\overrightarrow{AB}+\dfrac{3}{8}\overrightarrow{AB}+\dfrac{3}{8}\overrightarrow{AC}=-\dfrac{5}{8}\overrightarrow{AB}+\dfrac{3}{8}\overrightarrow{AC}\)
\(\overrightarrow{BK}=\overrightarrow{BA}+\overrightarrow{AK}=-\overrightarrow{AB}+\dfrac{3}{5}\overrightarrow{AC}=\dfrac{8}{5}\overrightarrow{BE}\)
\(\Rightarrow\) B, E, K thẳng hàng

Bài này có nhiều cách làm, vẽ thêm đường phụ cũng được, dùng định lý Menelaus cũng được nhưng lớp 10 thì nên dùng vecto
Ta có:
\(k=\dfrac{AG}{AB}=1-\dfrac{BG}{AB}=1-\dfrac{DE}{AB}=1-\dfrac{2DE}{3EF}\)
Đặt \(\dfrac{AD}{AM}=m\)
\(\Rightarrow\overrightarrow{ED}=m\overrightarrow{EM}+\left(1-m\right)\overrightarrow{EA}\)
\(=m\left(\overrightarrow{EC}+\overrightarrow{CM}\right)+\dfrac{1}{3}\left(m-1\right)\overrightarrow{AC}\)
\(=\dfrac{2}{3}m\overrightarrow{AC}+\dfrac{1}{2}m\overrightarrow{CB}+\dfrac{1}{3}\left(m-1\right)\overrightarrow{AC}\)
\(=\left(m-\dfrac{1}{3}\right)\overrightarrow{AC}+\dfrac{1}{2}m\overrightarrow{CB}\)
Lại có: \(\overrightarrow{EF}=\dfrac{2}{3}\overrightarrow{AB}=\dfrac{2}{3}\overrightarrow{AC}+\dfrac{2}{3}\overrightarrow{CB}\)
Mà \(D,E,F\) thẳng hàng nên:
\(\left(m-\dfrac{1}{3}\right)\dfrac{2}{3}=\dfrac{1}{2}m.\dfrac{2}{3}\Leftrightarrow m=\dfrac{2}{3}\)
\(\Rightarrow\overrightarrow{ED}=\dfrac{1}{2}\overrightarrow{EF}\Rightarrow ED=\dfrac{1}{2}EF\)\(\Leftrightarrow\dfrac{DE}{EF}=\dfrac{1}{2}\)
\(\Rightarrow k=\dfrac{2}{3}\)

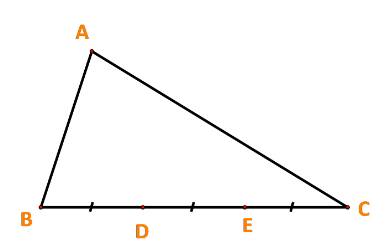
Ta có: \(\overrightarrow {AB} + \overrightarrow {BC} = \overrightarrow {AC} \Leftrightarrow \overrightarrow {BC} = \overrightarrow b - \overrightarrow a \)
Lại có: vecto \(\overrightarrow {BD} ,\overrightarrow {BC} \) cùng hướng và \(\left| {\overrightarrow {BD} } \right| = \frac{1}{3}\left| {\overrightarrow {BC} } \right|\)
\( \Rightarrow \overrightarrow {BD} = \frac{1}{3}\overrightarrow {BC} = \frac{1}{3}(\overrightarrow b - \overrightarrow a )\)
Tương tự: vecto \(\overrightarrow {BE} ,\overrightarrow {BC} \) cùng hướng và \(\left| {\overrightarrow {BE} } \right| = \frac{2}{3}\left| {\overrightarrow {BC} } \right|\)
\( \Rightarrow \overrightarrow {BE} = \frac{2}{3}\overrightarrow {BC} = \frac{2}{3}(\overrightarrow b - \overrightarrow a )\)
Ta có:
\(\overrightarrow {AB} + \overrightarrow {BD} = \overrightarrow {AD} \Leftrightarrow \overrightarrow {AD} = \overrightarrow a + \frac{1}{3}(\overrightarrow b - \overrightarrow a ) = \frac{2}{3}\overrightarrow a + \frac{1}{3}\overrightarrow b \)
\(\overrightarrow {AB} + \overrightarrow {BE} = \overrightarrow {AE} \Leftrightarrow \overrightarrow {AE} = \overrightarrow a + \frac{2}{3}(\overrightarrow b - \overrightarrow a ) = \frac{1}{3}\overrightarrow a + \frac{2}{3}\overrightarrow b \)

Lời giải:
\(\overrightarrow{BA}+\overrightarrow{BC}=\overrightarrow{BO}+\overrightarrow{OA}+\overrightarrow{BO}+\overrightarrow{OC}=2\overrightarrow{BO}+(\overrightarrow{OA}+\overrightarrow{OC})\)
\(=2\overrightarrow{BO}\) (do $\overrightarrow{OA}, \overrightarrow{OC}$ là 2 vecto đối)
Và:
\(\overrightarrow{BE}+\overrightarrow{BF}=\overrightarrow{BO}+\overrightarrow{OE}+\overrightarrow{BO}+\overrightarrow{OF}=2\overrightarrow{BO}+(\overrightarrow{OE}+\overrightarrow{OF})\)
\(=2\overrightarrow{BO}\) (do $\overrightarrow{OE}, \overrightarrow{OF}$ là 2 vecto đối)
Vậy \(\overrightarrow{BA}+\overrightarrow{BC}=\overrightarrow{BE}+\overrightarrow{BF}\)