Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

áp dụng định lí py-ta-go vào tam giác vuông , ta có:
AB2 + AC2 = BC2
hay : 62 + 82 = BC2
--->BC2 = 36 + 64
--->BC = \(\sqrt{100}\)
----> BC = 10( cm)
chúc bn học tốt ![]()

a/Áp dụng định lí Pytago và tam giác ABC vuông tại A:
BC2=AB2+AC2
=>AC2=BC2-AB2=102-62=100-36=64
=> AC=\(\sqrt{64}=8cm\)
b/ Xét tam giác ABC và tam giác ADC có:
AC chung
góc BAC=DAC=90 độ
AD=AB(gt)
=> Tam giác ABC=tam giác ADC(c-g-c)

a: \(\text{Δ}ABC\sim\text{Δ}HBA;\text{Δ}ABC\sim\text{Δ}HCA\)
b: \(BC=\sqrt{AB^2+AC^2}=25\left(cm\right)\)
\(AH=\dfrac{AB\cdot AC}{BC}=\dfrac{15\cdot20}{25}=12\left(cm\right)\)
\(BH=\dfrac{AB^2}{BC}=\dfrac{15^2}{25}=9\left(cm\right)\)
CH=BC-BH=25-9=16(cm)

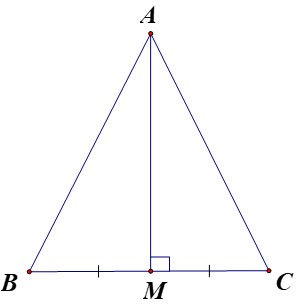
VÌ AM là đường phân giác đồng thời là trung tuyến nên tam giác ABC cân

a) Thấy 52=32+42 hay BC2=AB2+AC2
\(\Rightarrow\Delta ABC\) vuông tại A
b)Hình thì chắc bạn tự vẽ được nha![]()
![]()
![]()
Xét 2\(\Delta ABH\) và\(\Delta DBH\) có:
AB=DB
\(\widehat{BAH}=\widehat{BDH}\)
BH chung
\(\Rightarrow\Delta ABH=\Delta DBH\left(ch-cgv\right)\)
\(\Rightarrow\widehat{ABH}=\widehat{DBH}\)
\(\Rightarrow\)BH là tia phân giác \(\widehat{ABC}\)
c)tam giác ABC đã có các cạnh có độ dài khác nhau nên tam giác ABC ko cân được đâu chị
a) Ta có :
-BC2=52=25(1)
-AB2+AC2=32+42=25(2)
-Từ (1)và(2)suy ra BC2=AB2+AC2
-do đó tam giác ABC vuông tại A(áp dụng định lý Py-ta-go đảo)
-vậy tam giác ABC là tam giác vuông .
b)Xét \(\Delta\) ABH(vuông tại A) và \(\Delta\) DBH(vuông tại D) có
-BH là cạnh huyền chung
-AB=BD(gt)
-Do đó:\(\Delta\) ABH=\(\Delta\) DBH(cạnh huyền-cạnh góc vuông)
\(\Rightarrow\)Góc ABH =Góc DBH(hai góc tương ứng)
Vậy BH là tia phân giác của góc ABC

Đáp án B
Ta có
A M 2 + B C 2 2 = A B 2 B C . A B = A M 2 ⇒ B C . A B + B C 2 2 = A B 2 ⇔ A B B C 2 − A B B C − 1 4 = 0
⇔ q 2 = A B B C = 1 + 2 2 ⇔ q = 1 + 2 2

Đáp án B
Đặt B C = 2 x ⇒ A M = 2 q x , A B = 2 q 2 x .
Ta có: A B 2 = A M 2 + B M 2 ⇔ 2 q 2 x 2 = 2 q x 2 + x 2 ⇔ 4 q 4 − 4 q 2 − 1 = 0 ⇒ q 2 = 2 + 2 2 4
⇒ q = 2 + 2 2 2 .

Ta có: \(AB^2+AC^2=6^2+8^2=100\)
\(BC^2=10^2=100\)
\(\Delta ABC\) có \(AB^2+AC^2+BC^2\left(=100\right)\)
Theo định lí đảo Py-ta-go có \(\Delta ABC\) vuông tại A
Mà AM là đường trung tuyến của \(\Delta ABC\)
Do đó: \(AM=\frac{BC}{2}=5\left(cm\right)\)