Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bạn đổi D thành M nha
Gọi I là trung điểm của KC
Xét ΔKHC có M,I lần lượt là trung điểm của KH,KC
nên MI là đường trung bình
=>MI//HC
=>MI vuông góc với AH
Xét ΔAHI có
IM,HK là các đường cao
IM cắt HK tại M
Do đó: M là trực tâm
=>AM vuông góc với HI
Xét ΔBKC có
CH/CB=CI/CK
nên HI//BK
=>AM vuông góc với BK

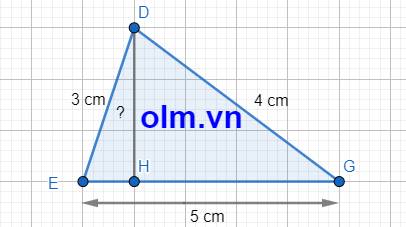
Gọi độ dài cạnh EH là \(x\) (cm); 0 < \(x< 5\)
Độ dài cạnh HG là: 5 - \(x\) (cm)
Xét tam giác vuông HDE vuông tại H, theo pytago ta có:
DH2 = 32 - \(x^2\) = 9 - \(x^2\)(1)
Xét tam giác vuông DHG vuông tại H theo pytago ta có:
DH2 = 42 - (5 - \(x\))2 = -\(x^2\) + 10\(x\) - 9(2)
Từ (1) và (2) ta có:
-\(x^2\) + 10\(x\) - 9 = 9 - \(x^2\)
10\(x\) = 18
\(x\) = 1,8 (thỏa mãn)
Thay \(x\) = 1,8 vào biểu thức (1) ta có:
DH2 = 9 - (1,8)2 = 5,76
DH = \(\sqrt{5,76}\) = 2,4 (cm)
Kết luận: độ dài đoạn DH là 2,4 cm

a) Xét tam giác DEG có:
M là trung điểm DE(gt)
MN//DG(gt)
=> N là trung điểm EG
b) Xét tam giác DEG có:
M là trung điểm DE(gt)
N là trung điểm EG(cmt)
=> MN là đường trung bình
\(\Rightarrow DG=2MN=2.5=10\left(cm\right)\)
a: Xét ΔDEG có
H là trung điểm của EG
HK//DG
Do đó: K là trung điểm của DE
Xét ΔDEG có
H là trung điểm của EG
K là trung điểm của DE
Do đó: HK là đường trung bình của ΔDEG