Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Khi n ngày càng lớn thì các giá trị \({u_n}\) ngày càng giảm tiến dần về gần trục Ox.
b)

Kể từ số hạng \({u_{1001}}\) trở đi thì khoảng cách từ \({u_n}\) đến 0 nhỏ hơn 0,001
Kể từ số hạng \({u_{10001}}\) trở đi thì khoảng cách từ \({u_n}\) đến 0 nhỏ hơn 0,0001

a) \({v_n} = {u_n} - 2 = \frac{{2n + 1}}{n} - 2 = \frac{{2n + 1 - 2n}}{n} = \frac{1}{n}\).
Áp dụng giới hạn cơ bản với \(k = 1\), ta có: \(\lim {v_n} = \lim \frac{1}{n} = 0\).
b) \({u_1} = \frac{{2.1 + 1}}{1} = 3,{u_2} = \frac{{2.2 + 1}}{2} = \frac{5}{2},{u_3} = \frac{{2.3 + 1}}{3} = \frac{7}{3},{u_4} = \frac{{2.4 + 1}}{4} = \frac{9}{4}\)
Biểu diễn trên trục số:
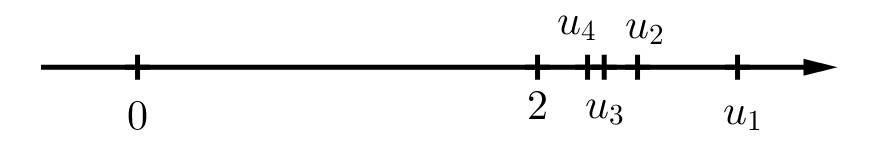
Nhận xét: Điểm \({u_n}\) càng dần đến điểm 2 khi \(n\) trở nên rất lớn.

Ta có: \({u_{n + 1}} = \frac{{\left( {n + 1} \right)a + 2}}{{\left( {n + 1} \right) + 1}} = \frac{{na + a + 2}}{{n + 1 + 1}} = \frac{{na + a + 2}}{{n + 2}}\)
Xét hiệu:
\(\begin{array}{l}{u_{n + 1}} - {u_n} = \frac{{na + a + 2}}{{n + 2}} - \frac{{na + 2}}{{n + 1}} = \frac{{\left( {na + a + 2} \right)\left( {n + 1} \right) - \left( {na + 2} \right)\left( {n + 2} \right)}}{{\left( {n + 2} \right)\left( {n + 1} \right)}}\\ = \frac{{\left( {{n^2}a + na + 2n + na + a + 2} \right) - \left( {{n^2}a + 2n + 2na + 4} \right)}}{{\left( {n + 2} \right)\left( {n + 1} \right)}}\\ = \frac{{{n^2}a + na + 2n + na + a + 2 - {n^2}a - 2n - 2na - 4}}{{\left( {n + 2} \right)\left( {n + 1} \right)}} = \frac{{a - 2}}{{\left( {n + 2} \right)\left( {n + 1} \right)}}\end{array}\)
a) Để \(\left( {{u_n}} \right)\) là dãy số tăng thì:
\({u_{n + 1}} - {u_n} > 0,\forall n \in {\mathbb{N}^*} \Leftrightarrow \frac{{a - 2}}{{\left( {n + 2} \right)\left( {n + 1} \right)}} > 0 \Leftrightarrow a - 2 > 0 \Leftrightarrow a > 2\)
b) Để \(\left( {{u_n}} \right)\) là dãy số giảm thì:
\({u_{n + 1}} - {u_n} < 0,\forall n \in {\mathbb{N}^*} \Leftrightarrow \frac{{a - 2}}{{\left( {n + 2} \right)\left( {n + 1} \right)}} < 0 \Leftrightarrow a - 2 < 0 \Leftrightarrow a < 2\)

a) Khoảng cách từ un tới 0 trở nên rất nhỏ (gần bằng 0) khi n trở nên rất lớn
b) Bắt đầu từ số hạng u100 của dãy số thì khoảng cách từ un đến 0 nhỏ hơn 0,01
Bắt đầu từ số hạng u1000 của dãy số thì khoảng cách từ un đến 0 nhỏ hơn 0,001

Đáp án đúng là: D
Ta có: un+1 = 2n+1+1 = 2n+2
Xét hiệu un+1 – un = 2n+2 – 2n = 3.2n > 0 với mọi n ∈ ℕ*
Vậy dãy số đã cho là dãy số tăng.

a) Ta có:
\(\begin{array}{l}{n^2} \ge 1\,\,\,\forall n \in {\mathbb{N}^*}\\ \Leftrightarrow {n^2} + 2 \ge 3\,\,\,\forall n \in {\mathbb{N}^*}\end{array}\)
Dãy số bị chặn dưới
b) Ta có:
\(\begin{array}{l} - 2n \ge - 2\,\,\,\forall n \in {\mathbb{N}^*}\\ \Leftrightarrow - 2n + 1 \ge - 1\,\,\,\forall n \in {\mathbb{N}^*}\end{array}\)
Dãy số bị chặn dưới
c) Ta có:
\(\begin{array}{l}{n^2} \ge 1\,\,\,\forall n \in {\mathbb{N}^*}\\ \Leftrightarrow {n^2} + n \ge 2\,\,\,\forall n \in {\mathbb{N}^*}\\ \Leftrightarrow 0 \le \frac{1}{{{n^2} + n}} \le \frac{1}{2}\,\,\,\forall n \in {\mathbb{N}^*}\end{array}\)
Dãy số bị chặn

a) \({u_n} = 3n - 2\)
\( \Rightarrow {u_1} = 3.1 - 2 = 1\)
\( \Rightarrow {u_2} = 3.2 - 2 = 4\)
\( \Rightarrow {u_3} = 3.3 - 2 = 7\)
\( \Rightarrow {u_4} = 3.4 - 2 = 10\)
\( \Rightarrow {u_5} = 3.5 - 2 = 13\)
\( \Rightarrow {u_{100}} = 3.100 - 2 = 298\)
b) \({u_n} = {3.2^n}\)
\( \Rightarrow {u_1} = {3.2^1} = 6\)
\( \Rightarrow {u_2} = {3.2^2} = 12\)
\( \Rightarrow {u_3} = {3.2^3} = 24\)
\( \Rightarrow {u_4} = {3.2^4} = 48\)
\( \Rightarrow {u_5} = {3.2^5} = 96\)
\( \Rightarrow {u_{100}} = {3.2^{100}}\)
c) \({u_n} = {\left( {1 + \frac{1}{n}} \right)^n}\)
\( \Rightarrow {u_1} = {\left( {1 + \frac{1}{1}} \right)^1} = 2\)
\( \Rightarrow {u_2} = {\left( {1 + \frac{1}{2}} \right)^2} = \frac{9}{4}\)
\( \Rightarrow {u_3} = {\left( {1 + \frac{1}{3}} \right)^3} = \frac{{64}}{{27}}\)
\( \Rightarrow {u_4} = {\left( {1 + \frac{1}{4}} \right)^4} = \frac{{625}}{{256}}\)
\( \Rightarrow {u_5} = {\left( {1 + \frac{1}{5}} \right)^5} = \frac{{7776}}{{3125}}\)
\( \Rightarrow {u_{100}} = {\left( {1 + \frac{1}{{100}}} \right)^{100}} = {\left( {\frac{{101}}{{100}}} \right)^{100}}\)

\(\forall n \in {\mathbb{N}^*}\) ta có:
\(\left. \begin{array}{l}1 > 0\\n > 0\end{array} \right\} \Leftrightarrow \frac{1}{n} > 0 \Leftrightarrow {u_n} > 0\)
\(n \ge 1 \Leftrightarrow {u_n} = \frac{1}{n} \le \frac{1}{1} \Leftrightarrow {u_n} \le 1\)





a) \(n = 100 \Leftrightarrow \left| {{u_{100}}} \right| = \left| {\frac{{{{\left( { - 1} \right)}^{100}}}}{{100}}} \right| = \frac{1}{{100}} = 0,01\)
\(n = 1000 \Leftrightarrow \left| {{u_{1000}}} \right| = \left| {\frac{{{{\left( { - 1} \right)}^{1000}}}}{{1000}}} \right| = \frac{1}{{1000}} = 0,001\)
Như vậy ta có thể điền vào bảng như sau:
b) \(\left| {{u_n}} \right| < 0,01 \Leftrightarrow \left| {\frac{{{{\left( { - 1} \right)}^n}}}{n}} \right| < 0,01 \Leftrightarrow \frac{1}{n} < 0,01 \Leftrightarrow n > 100\)
Vậy \(\left| {{u_n}} \right| < 0,01\) khi \(n > 100\).
\(\left| {{u_n}} \right| < 0,001 \Leftrightarrow \left| {\frac{{{{\left( { - 1} \right)}^n}}}{n}} \right| < 0,001 \Leftrightarrow \frac{1}{n} < 0,001 \Leftrightarrow n > 1000\)
Vậy \(\left| {{u_n}} \right| < 0,001\) khi \(n > 1000\).
c) Dựa vào trục số ta thấy, khoảng cách từ điểm \({u_n}\) đến điểm 0 trở nên rất bé khi \(n\) trở nên rất lớn.